Bài 1. Cho hai đường thẳng : \(y = (m – 1)x + 1\) (d1) và \(y = (2 – m)x + 2\) (d2) \((m ≠ 1, m ≠ 2)\)
a. Tìm m để hai đường thẳng song song
b. Chứng tỏ (d1) luôn đi qua 1 điểm cố định
c. Tìm m để hàm số \(y = (2 – m)x + 2\) đồng biến trên \(\mathbb R\)
d. Tìm m để (d2) qua điểm \(M(1; 2)\)
Bài 2. Cho hàm số \(y = -x + 1\)
a. Vẽ đồ thị của hàm số trên.
Từ đó suy ra đồ thị của hàm số \( y = \left| { – x + 1} \right|\)
b. Đồ thị của hàm số \(y = -x + 1\) cắt Ox, Oy lần lượt tại A và B. Tính diện tích tam giác OAB.
Advertisements (Quảng cáo)
Bài 1. a. (d1) // (d2) \( \Leftrightarrow \left\{ {\matrix{ {m – 1 = 2 – m} \cr {1 \ne 2} \cr } } \right. \Leftrightarrow m = {3 \over 2}\)
b. Gọi \(A({x_0}{\rm{; }}{y_0})\) là điểm cố định cần tìm.
(d1) qua A \( \Leftrightarrow {y_0} = \left( {m – 1} \right){x_0} + 1\) (với mọi m)
\( \Leftrightarrow {x_0}m + 1 – {y_0} – {x_0} = 0\) (với mọi m)
Advertisements (Quảng cáo)
Phương trình bậc nhất của m có vô số nghiệm
\( \Leftrightarrow \left\{ {\matrix{ {{x_0} = 0} \cr {1 – {y_0} – {x_0} = 0} \cr } } \right. \Leftrightarrow \left\{ {\matrix{ {{x_0} = 0} \cr {{y_0} = 1} \cr } } \right.\)
Vậy \(A(0; 1)\).
c. Hàm số \(y = (2 – m)x + 2\) đồng biến trên \(\mathbb R\) \(⇔ 2 – m > 0 ⇔ m < 2\)
d. \(M ∈ (d_2)\)\(\; ⇔ 2 = (2 – m).1 + 2 ⇔ m = 2\)
Bài 2. a. Bảng giá trị:
|
x |
1 |
0 |
|
y |
0 |
1 |
Đồ thị của hàm số là đường thẳng (d) qua hai điểm \(A(1; 0)\) và \(B(0; 1)\).
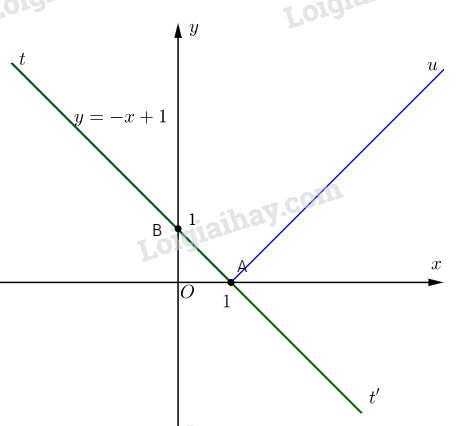
Ta có:
\( \eqalign{ & \left| {1 – x} \right| \cr&= \left\{ {\matrix{ { – x + 1\,\text{ nếu }\, – x + 1 \ge 0} \cr { – \left( { – x + 1} \right)\,\text{ nếu }\, – x + 1 < 0} \cr } } \right. \cr & = \left\{ {\matrix{ { – x + 1\,\text{ nếu }\,x \le 1} \cr {x – 1\,\text{ nếu }\,x > 1} \cr } } \right. \cr} \)
Vậy đồ thị của hàm số \( y = \left| { – x + 1} \right|\) được suy ra từ đồ thị của hàm số \(y = -x + 1\) bằng cách sau:
+ Tia At được giữ nguyên.
+ Lấy đối xứng tia At’ qua trục hoành, ta được đồ thị của hàm số \( y = \left| { – x + 1} \right|\) là đường gấp khúc tAu.
b. Ta có: \( {S_{OAB}} = {1 \over 2}OA.OB = {1 \over 2}\) (đvdt)
