Tóm tắt lý thuyết và Giải bài 26,27 trang 115; Bài 28, 29, 30, 31, 32 trang 116 SGK Toán 9 tập 1:Tính chất của hai tiếp tuyến cắt nhau – Luyện tập. Chương 2 hình học 9.
1. Định lý
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
– Điểm đó cách đều hai điểm.
– Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
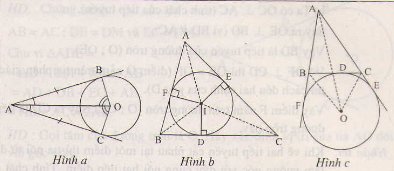
– Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm (h.a).
2. Đường tròn nội tiếp tam giác
Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác, còn tam giác gọi là ngoại tiếp đường tròn.
Tâm của đường tròn nội tiếp tam giác là giao điểm của các đường phân giác các góc trong của tam giác (h.b).
3. Đường tròn bàng tiếp tam giác
Đường tròn bàng tiếp tam giác là đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia.
Tâm của đường tròn bàng tiếp trong góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C, giao điểm này cùng nằm trên đường phân giác góc A (h.c).
Với một tam giác, có ba đường tròn bàng tiếp.
Hướng dẫn giải bài tập sách giáo khoa bài: Tính chất của hai tiếp tuyến cắt nhau lớp 9 trang 115, 116
Bài 26. Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
a) Chứng minh rằng OA vuông góc với BC.
b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO.
c) Tính độ dài các cạnh của tam giác ABC; biết OB=2cm, OA=4cm.
Giải.
a) Vì AB, AC là các tiếp tuyến của (O) nên AB=AC ⇒ ΔABC cân tại A.
Ta có AO là đường phân giác của góc ∠BAC của tam giác cân ABC nên AO cũng là đường cao.Suy ra OA ⊥ BC (tính chất của tam giác cân).
b) Gọi I là giao điểm của AO với BC
Ta có: ΔIBA = ΔICA (Cạnh huyền góc nhọn)
⇒IB = IC
Trong ΔBCD ta có:
IB = ID
OC = OD
} ⇒ OI là đường trung bình của Δ BCD
Nên OI//BD hay AO//BD
Vậy AO//BD(đpcm)
c) Vì AB là tiếp tuyển của (O) với B là tiếp điểm nên AB ⊥ OB và AB = AC
Vậy ΔOAB vuông tại B.
Áp dụng định lí Pytago trong tam giác vuông OAB, ta có:
Advertisements (Quảng cáo)
AO2 = AB2 + BO2
⇒ AB2 = AO2 – BO2 = 42 -22 = 12
⇒ AB = √12 = 2√3 (cm)
- Trong tam giác vuông OAB ta có
sinOAB = OB/OA =2/4 = 12
⇒ ∠OAB = 300 ⇒∠BAC = 2∠OAB =2.300 = 600
Tam giác ABC cân tại A và có ∠A = 600 nên ΔABC là tam giác đều. Suy ra AB= BC = CA = 2√3 (cm)
Nhận xét. Qua câu c) ta thấy: Góc tạo bởi hai tiếp tuyến của một đường tròn vẽ từ một điểm cách tâm một khoảng bằng đường kính đúng bằng 600.
Bài 27 trang 115. Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn O, nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và E. Chứng minh rằng chu vi tam giác ADE bằng 2AB.
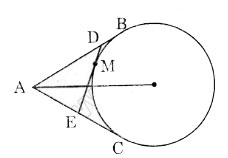
Ta có AB = AC; DB = DM;
EC = EM.
Chu vi Δ ADE:
AD +AE +DE = AD +DM + AE + EM
=AD + DB + AE + EC = AB + AC = 2AB
Bài 28. Cho góc xAy khác góc bẹt. Tâm của các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên đường nào?
Các đường tròn tiếp xúc với hai cạnh của một góc thì có tâm cách đều hai canh của góc đó. Vậy tâm của chúng nằm trên ta phân giác At của góc xAy.
Bài 29. Cho góc xAy khác góc bẹt, điểm B thuộc Ax. Hãy dựng đường tròn (O) tiếp xúc với Ax tại B và tiếp xúc với Ay.
Cách dựng:
– Dựng tia phân giác At của góc xAy
– Dựng đường thẳng Bz qua B và vuông góc với tia Ax
– Giao điểm O của At và Bz là tâm của đường tròn cần dựng.
– Dựng đường tròn tâm O, bán kính R = OB, ta được đường tròn cần dựng.
Luyện tập (Bài 30,31,32 trang 116 Toán 9 tập 1)
Bài 30 trang 116 Toán 9. Cho nửa đường tròn tâm O có đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax và By theo thứ tự ở C và D.
Chứng minh rằng:
a) ∠COD = 900
b) CD=AC+BD
c) Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn.
Advertisements (Quảng cáo)
Giải bài 30:
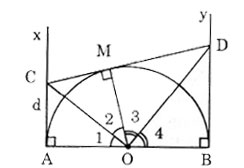a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.
Theo tính chất của 2 tiếp tuyến cắtnhau ta có:
CM = CA; DM = DB;
∠O1 = ∠O2; ∠O3 = ∠O4
⇒ ∠O2 + ∠O3 = ∠O1 + ∠O4 = 1800/2 = 900 (tính chất hai tia phân giác của hai góc kề bù).
⇒ ∠OCD = 900
b) CM và CA là hai tiếp tuyến của đường tròn, cắt nhau tại C nên CM = CA
Tương tự:
DM = DB
⇒ CM + DM = CA + DB
⇒ CD = AC + BD.
c) Ta có OM ⊥ CD
Trong tam giá vuông COD, OM Là đường cao thuộc cạnh huyển
OM2 = CM.DM
Mà OM = OA = OA = AB/2 và CM = AC; DM = BD
Suy ra AC.BD = AB2/2 = không đổi
Bài 31. Trên hình 82, tam giác ABC ngoại tiếp đường tròn (O).
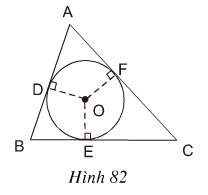
a) Chứng minh rằng:
2AD=AB+AC-BC.
b) Tìm các hệ thức tương tự hệ thức ở câu a).
a) Theo tính chất của 2 tiếptuyến cắt nhau ta có:
AD = AF; BD = BE; CF = CE.
Mặt khác:
AB = AD + BD (1)
AC = AF + CF = AD +CF (2)
BC = BE + CE = BD + CF (3)
Từ (1)+(2)-(3):
AB + AC – BC=
=(AD+DB)+(AD+FC)-( BD + CF)= 2AD.
b) Các hệ thức tương tự là:
2BE=2BD=BA+BC-AC;
2CF=2CE=CA+CB-AB.
Nhận xét. Từ bài toán trên ta có các kết quả sau:
AD=AF=p-a; BD=BE=p-b; CE=CF=p-c
trong đó AB=c; BC=a; CA=b và p là nửa chu vi của tam giác ABC.
Bài 32. Cho tam giác đều ABC ngoại tiếp đường tròn bán kính 1cm. Diện tích của tam giác ABC bằng:
(A) 6 cm2 ;
(B)√3 cm2 ;
(C) 3√3/4cm2
(D) 3√3cm2
Hãy chọn câu trả lời đúng.
Tâm O của đường tròn nội tiếp tam giác đều cũng là giao điểm ba đường trung tuyến, ba đường cao.
Do đó đường cao h=AE=3.OE=3cm.
Trong tam giác đều, h = a√3/2 (a là độ dài mỗi cạnh).
Suy ra
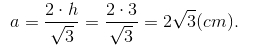
Do đó diện tích tam giác ABC là
Ta chọn (D).
