Chứng minh rằng: Đường thẳng đi qua trung điểm của đường trung bình và cắt hai đáy của hình thang thì chia hình thang thành hai đa giác có diện tích bằng nhau … trong Đề kiểm tra 15 phút môn Toán Chương 2 Hình học lớp 8 có đáp án. Xem Đề và đáp án đầy đủ phía dưới đây

Chứng minh rằng: Đường thẳng đi qua trung điểm của đường trung bình và cắt hai đáy của hình thang thì chia hình thang thành hai đa giác có diện tích bằng nhau.

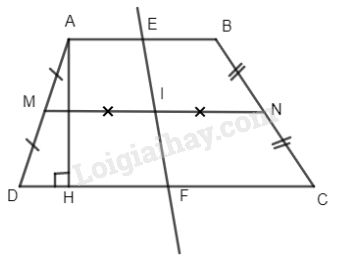
Gọi I là trung điểm của đường trung bình MN và đường thẳng EF đi qua I. Khi đó các tứ giác AEFD, BEFC cũng là các hình thang nên:
Advertisements (Quảng cáo)
\({S_{AEFD}} = {{\left( {AE + DF} \right).AH} \over 2} = MI.AH\)
(tính chất đường trung bình bằng nửa tổng hai cạnh đáy)
Tương tự \({S_{BEFC}} = {{\left( {BE + CF} \right).AH} \over 2} = NI.AI\)
Advertisements (Quảng cáo)
Mà MI = NI (gt)
\( \Rightarrow {S_{AEFD}} = {S_{BEFC}}.\)



![[THCS Hồng Dương] kiểm tra cuối năm môn Địa lớp 8: Vì sao tính chất nhiệt đới của miền Bắc và Đông Bắc Bắc Bộ bị giảm sút mạnh mẽ?](https://dethikiemtra.com/wp-content/uploads/2020/09/hinh-anh-dep-co-giao-dang-giang-bai_015649158-100x75.jpg)


