Gọi M, N theo thứ tự là các trung điểm của hai đáy AD và BC của hình thang ABCD. Từ điểm O tùy ý thuộc đoạn MN, kẻ đường thẳng song song với đáy hình thang, đường thảng này cắt các cạnh bên của hình thang tại E và F. Chứng minh rằng O là trung điểm của EF.
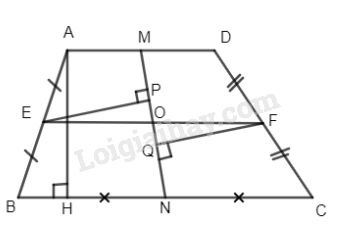
Ta có MA = MD, NB = NC (gt) và \(AD// BC.\)
Ta có:
\({S_{AMNB}} = {S_{DMNC}}\)
Advertisements (Quảng cáo)
(các hình thang có các đáy bằng nhau và chung đường cao)
Lại có \({S_{AEM}} = {S_{DFM}}\) (đáy AM = DM và đường cao từ E và F bằng nhau vì \(EF// AD\) ).
Tương tự \({S_{BEN}} = {S_{NFC}}\)
\( \Rightarrow {S_{AMNB}} – \left( {{S_{AEM}} + {S_{BEN}}} \right)\)\(\, = {S_{DMNC}} – \left( {{S_{BEN}} + {S_{NFC}}} \right)\)
Advertisements (Quảng cáo)
Hay \({S_{EMN}} = {S_{FMN}} \Rightarrow EP = FQ\)
Ta có \(\widehat {EOP} = \widehat {QOF}\) (đối đỉnh) và EP = FQ (cmt),
\(\widehat {EPO} = \widehat {FQO} = {90^ \circ }\)
Do đó \(\Delta EPO = \Delta FQO\left( {ch – gn} \right) \)
\(\Rightarrow OE = OF\) hay O là trung điểm của EF.
