Đề kiểm tra 15 phút môn Toán – Chương 1 Hình học 8: Chứng minh rằng: BD là tia phân giác của góc ADC

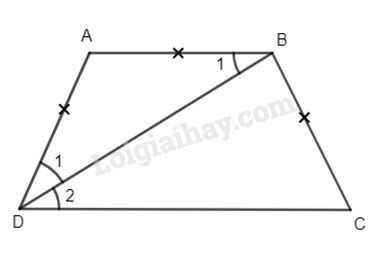
Cho hình thang ABCD \(\left( {AB//CD} \right)\) có \(\widehat D = {60^ \circ },AD = AB\)

a)Chứng minh rằng: BD là tia phân giác của góc ADC.

b)Chứng minh: \(BD \bot BC\)

a) Ta có:  \(\widehat {{B_1}} = \widehat {{D_2}}\) (so le trong) (1)

\(AB = AD(gt)\) nên \(\Delta ABD\) cân tại A

\( \Rightarrow \widehat {{B_1}} = \widehat {{D_1}}\) (2)

Từ (1) vào (2) suy ra \(\widehat {{D_1}} = \widehat {{D_2}}\) hay BD là tia phân giác của góc ADC.

b) Ta có: \(\widehat {BCD} = \widehat {ADC} = {60^ \circ }\) (hai góc kề đáy của hình thang cân)

mà BD là tia phân giác của góc ADC nên \(\widehat {{D_1}} = \widehat {{D_2}} = {30^ \circ }\)

Trong \(\Delta DBC\) ta có \(\widehat {DBC} = {180^ \circ } – \left( {\widehat {{D_2}} + \widehat {BCD}} \right)\)

\(\widehat {DBC} = {180^ \circ } – \left( {{{30}^ \circ } + {{60}^ \circ }} \right)\)

\(\widehat {DBC} = {90^ \circ },\) chứng tỏ \(BD \bot BC\)