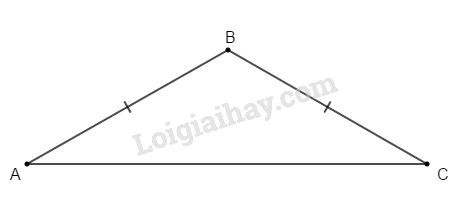
Bài 1: Cho tam giác ABC cân tại B có góc B tù.
a) So sánh độ dài hai cạnh AB và AC.
b) Biết số đo góc A bằng \({25^0}\). Tính số đo góc B và góc C.
Bài 2: Cho tam giác DEF có \(\widehat E = {90^0},\) tia phân giác DH. Qua H kẻ HI vuông góc với DF (I thuộc DF). Chứng minh:
a) \(\Delta DHE = \Delta DHI\).
b) DH là đường trung trực của đoạn EI.
c) \(EH < HF.\)

Bài 1:
Advertisements (Quảng cáo)
a) Ta có: \(\widehat B > \widehat A = \widehat C\) (vì \(\widehat B\) tù)
\( \Rightarrow AC > AB\) (quan hệ cạnh và góc)
b) Ta có \(\widehat A + \widehat B + \widehat C = {180^0}\) (tổng các góc trong tam giác)
mà \(\widehat A = \widehat C = {25^0}\)
\(\eqalign{ & \Rightarrow 2\widehat A + \widehat B = {180^0} \cr & \Rightarrow \widehat B = {130^0}. \cr} \)
Bài 2:
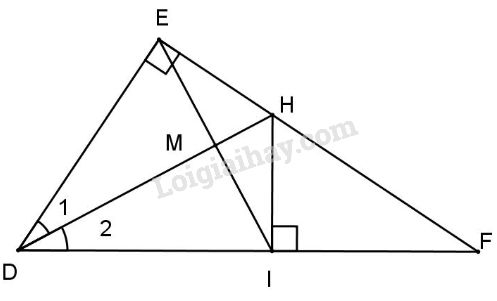
a) Xét \(\Delta DHE\) và \(\Delta DHI\) có
Advertisements (Quảng cáo)
+) \(\widehat {DEH} = \widehat {DIH} = {90^0}\) (gt)
+) DH: cạnh chung
+) \({\widehat D_1} = {\widehat D_2}\) (gt)
Do đó \(\Delta DHE = \Delta DHI\) (cạnh huyền góc nhọn).
b) Gọi M là giao điểm của EI và DH.
Xét \(\Delta DME\) và \(\Delta DMI\) có:
+) DM cạnh chung,
+) \({\widehat D_1} = {\widehat D_2}\) (gt);
+) DE = DI (cmt).
Do đó \(\Delta DME = \Delta DMI\) (c.g.c)
\( \Rightarrow \widehat {DME} = \widehat {DMI}\) mà \(\widehat {DME} + \widehat {DMI} = {180^0}\) (kề bù)
\( \Rightarrow \widehat {DME} = \widehat {DMI} = {90^0}\) hay \(DH \bot EI\)
Lại có \(ME = MI\) (cạnh tương ứng)
\( \Rightarrow DH\) là đường trung trực của đoạn EI.






