Tóm tắt kiến thức và Giải bài 1,2,3 trang 7; Bài 4 trang 8 SGK hình học 11: Phép tịnh tiến – Chương 1 Phép dời hình và phép đồng dạng trong mặt phẳng
A. Tóm tắt kiến thức phép tịnh tiến
1. Trong mặt phẳng có vectơ →v Phép biến hình biến mỗi đểm M thành điểm M’ sao cho →MM’= →v được gọi là phép tịnh tiến theo vectơ →v.
Phép tịnh tiến theo vectơ →v thường được kí hiệu là T→v , →v được gọi là vectơ tịnh tiến
từ đó suy ra MN = M’N’. Như vậy phép tịnh tiến là một phép biến hình bảo tồn khoảng cách
3. Phép tịnh tiến biến đường thẳng thành đường thằng song song hoặc trùng nhau với nó, biến đoạn thằng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn cùng bán kính.
4. Biểu thức tọa độ của phép tịnh tiến: Cho vectơ →v (a;b) và hai điểm M(x;y), M’ (x’; y’). Khi đó:
B. Hướng dẫn giải bài tập Sách giáo khoa trang 7,8 SGK hình học 11: Phép tịnh tiến
Bài 1. Chứng minh rằng: M’ =T→v (M) ⇔ M = (M’)
Bài 2. Cho tam giác ABC có G là trọng tâm. Xác định ảnh của tam giác ABC qua phép tịnh tiến theo vectơ →AG. Xác định điểm D sao cho phép tịnh tiến theo vectơ →AG biến D thành A.
Advertisements (Quảng cáo)
– Dựng hình bình hành ABB’G và ACC’G. Khi đó ta có →AG = →BB’ = →CC’ . Suy ra
Do đó ảnh của tam giác ABC qua phép tịnh tiến theo vectơ →AG
là tam giác GB’C’.
– Trên tia GA lấy điểm D sao cho A là trung điểm của GD. Khi đó ta có →DA = →AG. Do đó,
Bài 3 trang 7. Trong mặt phẳng tọa độ Oxy cho vectơ v = ( -1;2), hai điểm A(3;5), B( -1; 1) và đường thẳng d có phương trình x-2y+3=0.
a. Tìm tọa độ của các điểm A’, B’ theo thứ tự là ảnh của A, B qua phép tịnh tiến theo →v
b. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo →v
c. Tìm phương trình của đường thẳng d’ là ảnh của d qua phép tịnh tiến theo →v
Advertisements (Quảng cáo)
Giải: a) Giả sử A’=(x’; y’). Khi đó
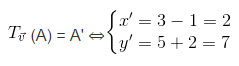
Do đó: A’ = (2;7)
Tương tự B’ =(-2;3)
b) Ta có A =T→v (C) ⇔ C=T→-v (A) = (4;3)
c)Cách 1. Dùng biểu thức tọa độ của phép tịnh tiến
Gọi M(x;y), M’ =T→v =(x’; y’). Khi đó x’ = x-1, y’ = y + 2 hay x = x’ +1, y= y’ – 2. Ta có M ∈ d ⇔ x-2y +3 = 0 ⇔ (x’+1) – 2(y’-2)+3=0 ⇔ x’ -2y’ +8=0 ⇔ M’ ∈ d’ có phương trình x-2y+8=0. Vậy T→v(d) = d’
Cách 2. Dùng tính chất của phép tịnh tiến
GọiT→v (d) =d’. Khi đó d’ song song hoặc trùng với d nên phương trình của nó có dạng x-2y+C=0. Lấy một điểm thuộc d chẳng hạn B(-1;1), khi đó T→v (B) = (-2;3) thuộc d’ nên -2 -2.3 +C =0. Từ đó suy ra C = 8.
Bài 4 trang 8. Cho hai đường thẳng a và b song song với nhau. Hãy chỉ ra một phép tịnh tiến biến a thành b. Có bao nhiêu phép tịnh tiến như thế?
Giả sử a và b có vectơ chỉ phương là →v
. Lấy điểm A bất kì thuộc a và điểm B bất kì thuộc b. Với mỗi điểm M, gọi M’ =T→AB (M) . Khi đó →MM’=→AB. Suy ra →AM=→BM’ Ta có:
M ∈ a ⇔ →AM cùng phương với →v ⇔→BM’ cùng phương với →v
⇔ M’ ∈ b.
Từ đó suy ra phép tịnh tiến theo →AB biến a thành b.
Vì A,B là các điểm bất kì ( trên a và b tương ứng) nên có vô số phép tịnh tiến biến a thành b.
