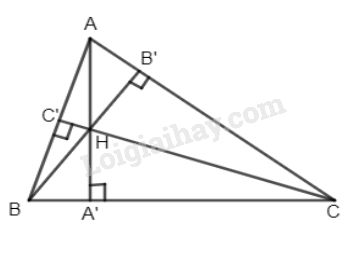
Cho tam giác ABC, các đường cao \(AA’,BB’,CC’\) cắt nhau tại H. Chứng minh rằng:
a) \(\dfrac{{{S_{HBC}}}}{{{S_{ABC}}}} = \dfrac{{HA’}}{{AA’}}\)
b) \(\dfrac{{HA’}}{{AA’}} + \dfrac{{HB’}}{{BB’}} + \dfrac{{HC’}}{{CC’}} = 1.\)
Advertisements (Quảng cáo)
a) Ta có: \({S_{HBC}} = \dfrac{1}{2}BC.HA’;\) \({S_{ABC}} = \dfrac{1}{2}BC.AA’\)
\( \Rightarrow \dfrac{{{S_{HBC}}}}{{{S_{ABC}}}} = \dfrac{{HA’}}{{AA’}}\)
b) Chứng minh tương tự câu a) ta có:
Advertisements (Quảng cáo)
\(\dfrac{{{S_{HAC}}}}{{{S_{ABC}}}} = \dfrac{{HB’}}{{BB’}}\) và \(\dfrac{{{S_{HAB}}}}{{{S_{ABC}}}} = \dfrac{{HC’}}{{CC’}}\)
Do đó: \(\dfrac{{{S_{HBC}} + {S_{HAC}} + {S_{HAB}}}}{{{S_{ABC}}}} \)\(\,= \dfrac{{HA’}}{{AA’}} + \dfrac{{HB’}}{{BB’}} + \dfrac{{HC’}}{{CC’}}\)
Hay \(1 = \dfrac{{HA’}}{{AA’}} + \dfrac{{HB’}}{{BB’}} + \dfrac{{HC’}}{{CC’}}\) (đpcm)
