Đề kiểm tra 15 phút môn Toán Chương 2 Hình học 8: Chứng minh tứ giác BCFE là hình chữ nhật

Cho tam giác ABC, lấy P, Q lần lượt là trung điểm cạnh AB và AC. Kẻ BE, CF cùng vuông góc với PQ.

a)Chứng minh tứ giác BCFE là hình chữ nhật.

b)Chứng minh \({S_{BCFE}} = {S_{ABC}}.\)

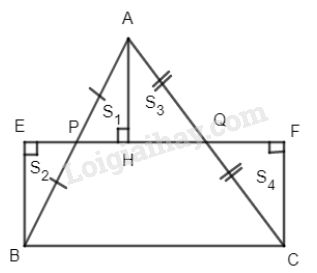
a) Ta có PQ là đường trung bình của \(\Delta ABC\) nên \(PQ// BC.\)

Lại có \(BE// CF\left( { \bot PQ} \right)\) nên BCFE là hình bình hành có một góc vuông.

Do đó BCFE là hình chữ nhật.

b) Kẻ \(AH \bot PQ.\) Ta có \(\Delta AHP = \Delta BEP\) (ch-gn)

Tương tự \(\Delta AHQ = \Delta CFQ\) (ch-gn)

Gọi \({S_1},{S_2},{S_3},{S_4}\) lần lượt là diện tích các tam giác AHP, BEP, AHQ và CFQ.

Ta có: \({S_1} = {S_2}\) và \({S_3} = {S_4}\)

Mà \({S_{BCEF}} = {S_2} + {S_{BPQC}} + {S_4}\) và \({S_{ABC}} = {S_1} + {S_{BPQC}} + {S_3}.\)

Do đó: \({S_{BCEF}} = {S_{ABC}}\).