Cho tứ giác ABCD. Gọi M là trung điểm của AB, N là trung điểm của CD. Chứng minh \({S_{BNDM}} = \dfrac{1}{2}{S_{ABCD}}.\) … trong Kiểm tra Toán 15 phút Chương 2 Hình học 8. Xem Đề và đáp án đầy đủ phía dưới đây
Cho tứ giác ABCD. Gọi M là trung điểm của AB, N là trung điểm của CD. Chứng minh \({S_{BNDM}} = \dfrac{1}{2}{S_{ABCD}}.\)
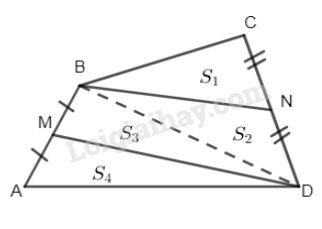
Nối BD, gọi diện tích các tam giác (theo hình vẽ) là \({S_1},{S_2},{S_3},{S_4}.\) Ta có BN là trung tuyến của \(\Delta BCD\) nên \({S_1} = {S_2}\) (chung đường cao, đáy bằng nhau)
Tương tự \({S_3} = {S_4}\)
Advertisements (Quảng cáo)
\( \Rightarrow {S_2} + {S_3} = {S_1} + {S_4} = {1 \over 2}{S_{ABCD}}\)
Hay \({S_{BNDM}} = {1 \over 2}{S_{ABCD.}}\)
Advertisements (Quảng cáo)
