Đề kiểm tra 15 phút môn Toán Chương 1 Hình học 8: Chứng minh ACFE là hình thang cân?

Cho tam giác đều ABC. Vẽ đường vuông góc với BC tại C cắt AB tại E. Vẽ đường vuông góc với AB tại A cắt BC tại F. Chứng minh ACFE là hình thang cân.

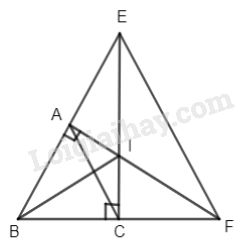
Gọi I là giao điểm của AF và CE.

Ta có hai tam giác vuông BAI và BCI bằng nhau (cạnh huyền- cạnh góc vuông) \( \Rightarrow IA = IC\)

Xét hai tam giác vuông AIE và CIF, ta có:

IA = IC (cmt)

\(\widehat {AIE} = \widehat {CIF}\)(đối đỉnh)

\(\widehat {IAE} = \widehat {ICF} = {90^ \circ }\)

Suy ra \(\Delta AIE = \Delta CIF(g.c.g)\)

\(\Rightarrow AE = CF\) ( hai cạnh tương ứng)

Mà BA = BC (gt)

\( \Rightarrow AE + BA = CF + BC\) hay BE = BF.

Do đó \(\Delta EBF\) cân có \(\widehat B = {60^ \circ }(gt)\) nên đều \( \Rightarrow \widehat E = \widehat F = {60^ \circ }\)

\( \Rightarrow \widehat E = \widehat {BAC} \Rightarrow AC// EF\) (cặp góc đồng vị bằng nhau) hay ACFE là hình thang cân.