Đề kiểm tra 15 phút môn Toán Chương 1 Hình học 9: Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45˚

Bài 1. Cho \(∆ABC\) vuông tại A, biết \(AB = 9cm, BC = 15cm\). Tính các tỉ số lượng giác của hai góc B và C.

Bài 2. Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45˚: \(\cos60^o;\sin65^o;\cos55^o10′;\tan75^o;\)\(\cot80^o.\)

Bài 1.

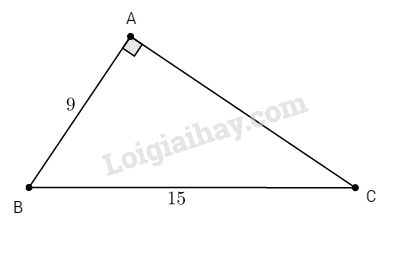
Ta có: \(A{C^2} = \sqrt {B{C^2} – A{B^2}}  \)\(\;= \sqrt {{{15}^2} – {9^2}}  = 12\,\left( {cm} \right)\)

\(\eqalign{  & {\mathop{\rm sinB}\nolimits}  = {{AC} \over {BC}} = {{12} \over {15}} = {4 \over 5} \cr&\Rightarrow {\mathop{\rm cosC}\nolimits}  = {4 \over 5}  \cr  & {\mathop{\rm cosB}\nolimits}  = {{AB} \over {BC}} = {9 \over {15}} = {3 \over 5}\cr& \Rightarrow \sin C = {3 \over 5}  \cr  & \tan B = {{AC} \over {AB}} = {{12} \over 9} = {4 \over 3}\cr& \Rightarrow \cot C = {4 \over 3}  \cr  & \cot B = {{AB} \over {AC}} = {3 \over 4}\cr& \Rightarrow \tan C = {3 \over 4}. \cr} \)

Bài 2.  \(\eqalign{  & \cos 60^\circ  = \sin \left( {90^\circ  – 60^\circ } \right) = \sin 30^\circ   \cr  & \sin 65^\circ  = \cos \left( {90^\circ  – 65^\circ } \right) = \cos 25^\circ   \cr  & \cos 55^\circ 10′ = \sin \left( {90^\circ  – 55^\circ 10′} \right) \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= \sin 34^\circ 50′  \cr  & \tan 75^\circ  = \cot \left( {90^\circ  – 75^\circ } \right) = \cot 15^\circ   \cr  & \cot 80^\circ  = \tan \left( {90^\circ  – 80^\circ } \right) = \tan 10^\circ  \cr} \)