
Bài 1. Viết phương trình đường thẳng (d) đi qua hai điểm A(0; -3) và B(1; -1)
Bài 2. Cho his đường thẳng d1 : \(y = mx + m + 2\) và d2 : \(y = -x\). Tìm m để d1 và d2 song song.
Bài 3. Cho hàm số \(y = {4 \over 3}x + 4\)
a. Vẽ đồ thị hàm số
b. Tìm tọa độ giao điểm A, B của đồ thị lần lượt với Ox và Oy. Tính diện tích tam giác OAB (đơn vị đo trên các trục tọa độ là xăng-ti-mét).

Bài 1. Phương trình đường thẳng d có dạng: \(y = ax + b\)
Advertisements (Quảng cáo)
\(A \in \left( d \right) \Rightarrow – 3 = a.0 + b \Rightarrow b = – 3.\)
Khi đó : \(y = ax – 3\)
\(B \in \left( d \right) \Rightarrow – 1 = a.1 – 3 \Rightarrow a = 2\)
Vậy phương trình của d là : \(y = 2x – 3\)
Bài 2. d1 // d2
Advertisements (Quảng cáo)
\(\Leftrightarrow \left\{ {\matrix{ {m = – 1} \cr {m + 2 \ne 0} \cr } } \right. \Leftrightarrow m = – 1\)
Bài 3. a. Bảng giá trị:
|
x |
-3 |
0 |
|
y |
0 |
4 |
Đồ thị của hàm số \(y = {4 \over 3}x + 4\) là đường thẳng qua hai điểm \(A(-3; 0)\) và \(B(0;4)\)
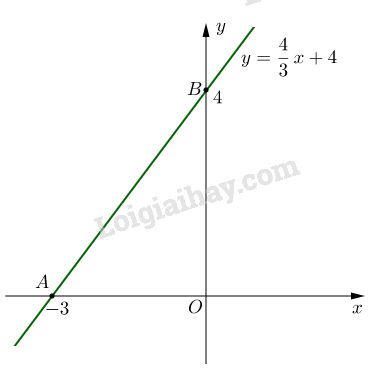
b. Ta có: \(A(-3; 0)\) và \(B(0; 4)\)
\( \Rightarrow OA = \left| { – 3} \right| = 3\) và \(OB = 4\).
Diện tích \(\Delta OAB:S = {1 \over 2}.OA.OB = {1 \over 2}.3.4 = 6\)\(\,\left( {c{m^2}} \right)\)



![[Quận Thủ Đức] thi kì 2 môn Lý lớp 9: Cấu tạo của máy phát điện xoay chiều gồm có những bộ phận chính nào?](https://dethikiemtra.com/wp-content/uploads/2020/07/82208322_457565911818124_3698770116704468992_n-100x75.jpg)


