Tóm tắt kiến thức và giải bài tập trong sách giáo khoa. Bài 1,2,3 trang 49; bài 4 trang 50 SGK đại số 10: Hàm số bậc 2 – Chương 2.
A. Tóm tắt kiến thức hàm số bậc 2 – Đại số 10
Hàm số bậc hai là hàm số có công thức: y = ax2 + bx + c (a ≠ 0) có miền xác định D = R.
Bảng biến thiên:
 Trong đó ∆ = b2 – 4ac.
Trong đó ∆ = b2 – 4ac.
Đồ thị hàm số y = ax2 + bx + c (a ≠ 0) là đường thẳng parabol có: đỉnh I (-b/2a; -∆/4a), trục đối xứng là đường thẳng x =-b/2a.
Giao điểm với trục : A(0; c). Hoành độ giao điểm với trục hoành là nghiệm của ax2 + bx + c = 0.
Đồ thị hàm số y = ax2 + bx + c (a ≠ 0) suy ra từ đồ thị hàm số y = ax2 bằng cách:
Tịnh tiến song song với trục hoành |b/2a| đơn vị bên trái nếu b/2a > 0, về bên phải nếu b/2a < 0.
+ Tịnh tiến song song với trục tung |-∆/4a| đơn vị lên trên nếu -∆/4a > 0, và xuống dưới nếu -∆/4a < 0.
B. Đáp án và hướng dẫn giải bài hàm số bậc 2 trang 49, 50 Đại số 10
Bài 1. Xác định tọa độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của mỗi parabol.
a) y = x2 – 3x + 2; b) y = – 2x2 + 4x – 3;
c) y = x2 – 2x; d) y = – x2 + 4.
Đáp án: a) y = x2 – 3x + 2. Hệ số: a = 1, b = – 3, c = 2.
- Hoành độ đỉnh x1 = -b/2a = -3/2
- Tung độ đỉnh

Vậy đỉnh parabol là I (3/2; -1/4).
- Giao điểm của parabol với trục tung là A(0; 2).
- Hoành độ giao điểm của parabol với trục hoành là nghiệm của phương trình:

Vậy các giao điểm của parabol với trục hoành là B(1; 0) và C(2; 0).
Tương tự các em áp dụng giải ý b,c,d:
b) y = – 2x2 + 4x – 3: Đỉnh I(1; 1). Giao điểm với trục tung A(0;- 3).
Phương trình – 2x2 + 4x – 3 = 0 vô nghiệm. Không có giao điểm cuả parabol với trục hoành.
c) y = x2 – 2x: Đỉnh I(1;- 1). Các giao điểm với hai trục tọa độ: A(0; 0), B(2; 0).
d)y = – x2 + 4: Đỉnh I(0; 4). Các giao điểm với hai trục tọa độ: A(0; 4), B(- 2; 0), C(2; 0).
Bài 2. Lập bảng biến thiên và vẽ đồ thị của các hàm số.
Advertisements (Quảng cáo)
a) y = 3x2– 4x + 1; b) y = – 3x2 + 2x – 1;
c) y = 4x2– 4x + 1; d) y = – x2 + 4x – 4;
e) y = 2x2+ x + 1; f) y = – x2 + x – 1.
Đáp án: a) Bảng biến thiên: 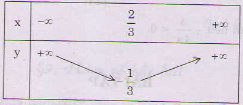
Đồ thị: – Đỉnh: I(2/3;-1/3)
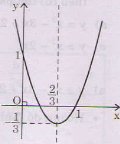 Đồ thị hàm số y = 3×2- 4x + 1
Đồ thị hàm số y = 3×2- 4x + 1
– Trục đối xứng: x=2/3
– Giao điểm với trục tung A(0; 1)
– Giao điểm với trục hoành B(1/3;0), C(1; 0).
b) y = – 3x2 + 2x – 1= -3 (x -1/3)2 – 2/3
Bảng biến thiên:
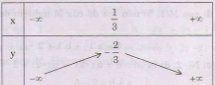
Advertisements (Quảng cáo)
Vẽ đồ thị: – Đỉnh I(1/3;-2/3)
Trục đối xứng: x=1/3.
– Giao điểm với trục tung A(0;- 1).
– Giao điểm với trục hoành: không có.
Ta xác định thêm mấy điểm: B(1;- 2), C(1;- 6). (học sinh tự vẽ).
c) y = 4x2 – 4x + 1 = 4(x-1/2)2.
Lập bảng biến thiên và vẽ tương tự câu a, b.
d) y = – x2 + 4x – 4 = – (x – 2)2
Bảng biến thiên:
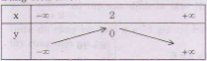
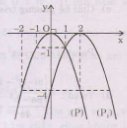 Đồ thị hàm số y = – x2 + 4x – 4 = – (x – 2)2
Đồ thị hàm số y = – x2 + 4x – 4 = – (x – 2)2
Cách vẽ đồ thị:
Ngoài cách vẽ như câu a, b, ta có thể vẽ như sau:
+ Vẽ đồ thị (P) của hàm số y = – x2.
+ Tịnh tiến (P) song song với Ox sang phải 2 đơn vị được (P1) là đồ thị cần vẽ.
e), g) học sinh tự giải.
Bài 3. Xác định parabol y = ax2 + bx + 2, biết rằng parabol đó:
a) Đi qua hai điểm M(1; 5) và N(- 2; 8);
b) Đi qua hai điểm A(3;- 4) và có trục đối xứng là x=-3/2
c) Có đỉnh là I(2;- 2);
d) Đi qua điểm B(- 1; 6) và tung độ của đỉnh là -1/4
Giải bài 3: a) Vì parabol đi qua M(1; 5) nên tọa độ của M nghiệm đúng phương trình của parabol: 5 = a.12 + b.1 + 2.
Tương tự, với N(- 2; 8) ta có: 8 = a.(- 2)2 + b.(- 2) + 2
Giải hệ phương trình: 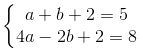 ta được a = 2, b = 1.
ta được a = 2, b = 1.
Parabol có phương trình là: y = 2x2 + x + 2.
Tương tự các em áp dụng cách giải câu a để làm các câu tiếp theo
b) Giải hệ phương trình: 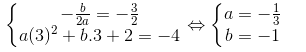 Parabol: y = -1/3 x2 – x + 2.
Parabol: y = -1/3 x2 – x + 2.
c) Giải hệ phương trình: 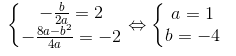 Parabol: y = x2 – 4x + 2.
Parabol: y = x2 – 4x + 2.
d) Ta có: 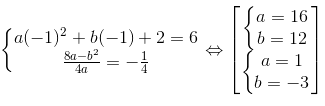
Parabol: y = 16x2 + 12x + 2 hoặc y = x2 – 3x + 2.
Bài 4 trang 50. Xác định a, b, c, biết parabol y = ax2 + bx + c đi qua điểm A(8; 0) và có đỉnh I(6; – 12).
Đáp án: Tương tự như cách giải bài 3(ở trên)
Ta có hệ phương 3 phương trình:
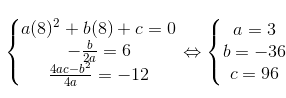
Parabol: y = 3x2 – 36x + 96.






