
1. a. Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {x^2} + 4x\) .
b. Tìm các giá trị của m để phương trình \(\left| x \right|\left( {x + 4} \right) + m = 0\) có ba nghiệm phân biệt.
2. a. Giải và biện luận phương trình \(\left| {mx + 2} \right| = \left| {2x – m} \right|\) .
b. Xác định m để phương trình \(\dfrac{{2x – m + 1}}{{\sqrt {x – 1} }} – 4\sqrt {x – 1} = \dfrac{{x – 2m + 1}}{{\sqrt {x – 1} }}\) có nghiệm.
3. Cho phương trình \({x^2} – 2\left( {m + 1} \right)x + 4m – 3 = 0{\rm{ (1)}}\) .
a. Chứng minh rằng phương trình (1) luôn có hai nghiệm phân biệt với mọi giá trị của m.
b. Xác định m để hai nghiệm x1, x2 của phương trình thỏa mãn điều kiện \(x_1^2 + x_2^2 = 14\) .

1. a. Xét hàm số \(y = {x^2} + 4x\).
Tập xác định \(\mathbb R\)
Đồ thị parabol có
+ Đỉnh \(I(-2;-4)\)
+ Trục đối xứng \(x= -2\)
+ Cắt Oy tại \((0;0)\), cắt Ox tại \((0;0)\) và \((-4;0).\)
Bảng biến thiên

Đồ thị
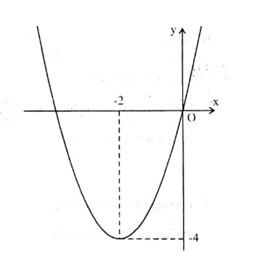
b. Ta có \(\left| x \right|\left( {x + 4} \right) + m = 0\)
\(\Leftrightarrow \left| x \right|\left( {x + 4} \right) = – m\) .
Advertisements (Quảng cáo)
Phương trình trên là phương trình hoành độ giao điểm của đồ thị hàm số \(y = \left| x \right|\left( {x + 4} \right)\) và đường thẳng y= -m.
Ta có
\(y = \left| x \right|\left( {x + 4} \right)\)\(\; = \left\{ \matrix{ {x^2} + 4x{\rm{ \text{ khi } x}} \ge {\rm{0 }} \hfill \cr {\rm{ – }}\left( {{x^2} + 4x} \right){\rm{\text{ khi }x < 0}} \hfill \cr} \right.\).
Suy ra đồ thị hàm số này gồm phần đồ thị hàm số \(y = {x^2} + 4x\) khi \(x \ge 0\) và phần đối xứng với đồ thị này qua trục Ox khi \(x<0.\)

Theo đồ thị phương trình có ba nghiệm phân biệt khi và chỉ khi
\(0 < – m < 4 \Leftrightarrow – 4 < m < 0\) .
2. a.Ta có:\(\left| {mx + 2} \right| = \left| {2x – m} \right| \)
\(\Leftrightarrow \left[ \matrix{ mx + 2 = 2x – m \hfill \cr mx + 2 = – 2x + m \hfill \cr} \right.\)
Với: \(mx + 2 = 2x – m\)
\(\Leftrightarrow \left( {m – 2} \right)x = – \left( {m + 2} \right)\) (1)
+ \(m – 2 \ne 0 \Leftrightarrow m \ne 2\) : Phương trình (1) có nghiệm \(x = – \dfrac{{m + 2}}{{m – 2}}\)
+ \(m – 2 = 0 \Leftrightarrow m = 2\) : Phương trình trở thành \(0x= -4\). Phương trình này cô nghiệm.
Advertisements (Quảng cáo)
Với: \(mx + 2 = – 2x + m \)\(\,\Leftrightarrow \left( {m + 2} \right)x = m – 2\) (2)
+ \(m + 2 \ne 0 \Leftrightarrow m \ne – 2\) : Phương trình (2) có nghiệm \(x = \dfrac{{m – 2}}{{m + 2}}\)
+ \(m + 2 = 0 \Leftrightarrow m = – 2\) : Phương trình trở thành \(0x = – 4\) . Phương trình này vô nghiệm.
Ta có \( – \dfrac{{m + 2}}{{m – 2}} = \dfrac{{m – 2}}{{m + 2}}\)
\(\Leftrightarrow – {\left( {m + 2} \right)^2} = {\left( {m – 2} \right)^2}\)
\(\Leftrightarrow 2{m^2} + 8 = 0\)
Phương trình này vô nghiệm nên khả năng này không xảy ra.
Kết luận:
\(m \ne \pm 2\) : Hai nghiệm \(x_1 = – \dfrac{{m + 2}}{{m – 2}},x_1 = \dfrac{{m – 2}}{{m + 2}}\)
\(m = \pm 2\) : Một nghiệm \(x = 0\) .
b. Xét phương trình \(\dfrac{{2x – m + 1}}{{\sqrt {x – 1} }} – 4\sqrt {x – 1} = \dfrac{{x – 2m + 1}}{{\sqrt {x – 1} }}\)
Điều kiện xác định \(x – 1 > 0 \Leftrightarrow x > 1.\)
Với điều kiện xác định đó thì phương trình tương đương
\(2x + m + 1 – 4\left( {x – 1} \right) = x – 2m + 1 \)
\(\Leftrightarrow 3x = 3m + 4 \)
\(\Leftrightarrow x = \dfrac{3m + 4}{ 3}\) .
Phương trình đã cho có nghiệm khi nghiệm trên thỏa mãn điều kiện \(x> 1\)
\(\dfrac{{3m + 4}}{3} > 1 \Leftrightarrow m > – \dfrac{1}{3}\)
Kết luận: Phương trình có nghiệm khi \(m > – \dfrac{1}{3}\)
3. a. Xét phương trình \({x^2} – 2\left( {m + 1} \right)x + 4m – 3 = 0{\rm{ (1)}}\).
Ta có \(\Delta ‘ = {\left( {m + 1} \right)^2} – \left( {4m – 3} \right) \)\(\,= {m^2} – 2m + 4 = {\left( {m – 1} \right)^2} + 3 > 0,\forall m\) .
Vậy phương trình (1) luôn có hai nghiệm phân biệt với mọi giá trị của m.
b.Theo định lí Viet \({x_1} + {x_2} = 2\left( {m + 1} \right),{x_1}{x_2} = 4m – 3\) .
Suy ra \(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} – 2{x_1}{x_2} \)\(\,= 4{\left( {m + 1} \right)^2} – 2\left( {4m – 3} \right) = 4{m^2} + 10\) .
Do đó: \(x_1^2 + x_2^2 = 14 \Leftrightarrow 4{m^2} + 10 = 14\)
\(\Leftrightarrow {m^2} = 1 \Leftrightarrow m = \pm 1\)






