1. a. Vẽ đồ thị hàm số \(y = – {x^2} + 4x – 3\) .
b. Xác định các giá trị của m để phương trình \({x^2} – 4\left| x \right| + m = 0\) có ít nhất ba nghiệm.
2. a. Giải phương trình \({x^2} + {\left( {\dfrac{x}{{x + 1}}} \right)^2} = 3\)
b. Tìm m để phương trình \(\dfrac{{x + m – 1}}{{x + 1}} + \dfrac{{x – 2}}{x} = 2\) vô nghiệm.
3. Hai nghiệm x1, x2 của một phương trình bậc hai thoả mãn các hệ thức \({x_1} + {x_2} + {x_1}{x_2} = 0\) và \(\left( {m – 1} \right)\left( {{x_1} + {x_2}} \right) – {x_1}{x_2} = 3m – 1\)
Lập phương trình bậc hai đó.
4. Xác định m để phương trình \(2x + \sqrt {x – 1} = m – 1\) có nghiệm.

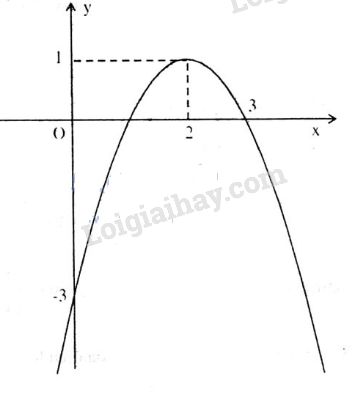
1. a. Hàm số \(y = – {x^2} + 4x – 3\) có đồ thị là một parabol với
+ Đỉnh \(I(2;1)\)
+ Trục đối xứng \(x= 2\)
+ Cắt Oy tại \(\left( {0;3} \right)\) , cắt Ox tại \(\left( {0;1} \right)\) và \(\left( {0;1} \right)\).
Đồ thị
b. Ta có \({x^2} – 4\left| x \right| + m = 0\)
\(\Leftrightarrow – {x^2} + 4\left| x \right| – 3 = m – 3\) .
Phương trình trên là phương trình hoành độ giao điểm của đồ thị hàm số \(y = – {x^2} + 4\left| x \right| – 3\) và đường thẳng \(y = m – 3\) .
Hàm số \(y = – {x^2} + 4\left| x \right| – 3\) là hàm số chẵn nên đồ thị đối xứng qua trục tung.
Khi \(x \ge 0\) thì hàm số trở thành \(y = – {x^2} + 4x – 3\) .
Do đó đồ thị hàm số của hàm số \(y = – {x^2} + 4\left| x \right| – 3\) bao gồm phần đồ thị hàm số \(y = – {x^2} + 4x – 3\) ở bên phải trục tung và phần đối xứng của nó qua trục tung.
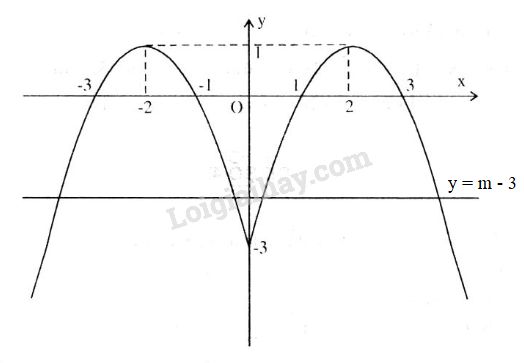
Theo đồ thị phương trình có ít nhất ba nghiệm khi và chỉ khi
\( – 3 \le m – 3 < 1 \Leftrightarrow 0 \le m < 4\) .
Advertisements (Quảng cáo)
2. a. Xét phương trình \({x^2} + {\left( {\dfrac{x}{{x + 1}}} \right)^2} = 3\)
Điều kiện xác định \(x + 1 \ne 0 \Leftrightarrow x \ne – 1\) .
Ta có:
\(\eqalign{ & {x^2} + {\left( {{x \over {x + 1}}} \right)^2} = 3 \cr&\Leftrightarrow {\left( {x – {x \over {x + 1}}} \right)^2} + 2x.{x \over {x + 1}} = 3 \cr & {\rm{ }} \Leftrightarrow {\left( {{{{x^2}} \over {x + 1}}} \right)^2} + 2.{{{x^2}} \over {x + 1}} – 3 = 0 \cr} \) .
Đặt \(t = \dfrac{{{x^2}}}{{x + 1}}\) , phương trình trở thành: \({t^2} + 2t – 3 = 0\)
\(\Leftrightarrow \left[ \matrix{ t = 1 \hfill \cr t = – 3 \hfill \cr} \right.\)
+) \(\dfrac{{{x^2}}}{{x + 1}} = 1 \Leftrightarrow {x^2} – x – 1 = 0\)
\(\Leftrightarrow x = \dfrac{{1 \pm \sqrt 5 }}{2}\) (thỏa mãn điều kiện).
+) \(\dfrac{{{x^2}}}{{x + 1}} = – 3 \Leftrightarrow {x^2} + 3x + 3 = 0\) Vô nghiệm.
Vậy phương trình có hai nghiệm \(x = \dfrac{{1 \pm \sqrt 5 }}{2}\)
b.Xét phương trình \(\dfrac{{x + m – 1}}{{x + 1}} + \dfrac{{x – 2}}{x} = 2\) (1).
Điều kiện xác định \(\left\{ \matrix{ x \ne – 1 \hfill \cr x \ne 0 \hfill \cr} \right.\) .
Với điều kiện trên thì phương trình tương đương
\({x^2} + \left( {m – 1} \right)x + {x^2} – x – 2 = 2{x^2} + 2x\)
\(\Leftrightarrow \left( {m – 4} \right)x = 2\) (2).
Advertisements (Quảng cáo)
Phương trình (1) vô nghiệm khi và chỉ khi phương trình (2) vô nghiêm hoặc có nghiệm không thỏa mãn điều kiện.
+ Phương trình (2) vô nghiệm khi và chỉ khi \(m – 4 = 0 \Leftrightarrow m = 4\) .
+ Phương trình (2) có nghiệm khi và chỉ khi \(m – 4 \ne \Leftrightarrow m \ne 4\) .
Khi đó nghiệm của (2) là \(x = \dfrac{2}{{m – 4}}\) . Hiển nhiên \(\dfrac{2}{{m – 4}} \ne 0\)
Nghiệm này không thỏa mãn điều kiện khi và chỉ khi
\(\dfrac{2}{{m – 4}} = – 1\)
\(\Leftrightarrow 2 = – m + 4 \Leftrightarrow m = 2\)
Vậy phương trình (1) vô nghiệm khi và chỉ khi m= 4 hoặc m= 2.
3. Xét hệ \(\left\{ \matrix{ {x_1} + {x_2} + {x_1}{x_2} = 0 \hfill \cr \left( {m – 1} \right)\left( {{x_1} + {x_2}} \right) – {x_1}{x_2} = 3m – 1 \hfill \cr} \right.\)
Đặt \(S = {x_1} + {x_2},P = {x_1}{x_2}\) .
Hệ trở thành \(\left\{ \matrix{ S + P = 0 \hfill \cr \left( {m – 1} \right)S – P = 3m – 1 \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{ mS = 3m – 1 \hfill \cr P = – S \hfill \cr} \right.\)
Để hệ có nghiệm thì \(m \ne 0\) . Khi đó:
\(\left\{ \begin{gathered}
S = \frac{{3m – 1}}{m} \hfill \\
P = – \frac{{3m – 1}}{m} \hfill \\
\end{gathered} \right.\)
Vậy phương trình bậc hai cần tìm là
\(\eqalign{ & {x^2} – {{3m – 1} \over m}x – {{3m – 1} \over m} = 0 \cr & \Leftrightarrow m{x^2} – \left( {3m – 1} \right)x – 3m + 1 = 0 \cr} \) .
4. Xét phương trình \(2x + \sqrt {x – 1} = m – 1\) (1)
Điều kiện xác định: \(x – 1 \ge 0 \Leftrightarrow x \ge 1\) .
Đặt \(t = \sqrt {x – 1} ,t \ge 0\) . Phương trình trở thành
\(2\left( {{t^2} + 1} \right) + t = m – 1 \)
\(\Leftrightarrow 2{t^2} + t + 3 – m = 0\) (2).
Phương trịnh (1) có nghiệm khi và chỉ khi phương trình (2) có nghiệm \(t \ge 0\) .
Có hai trường hợp
+ Phương trình (2) có hai nghiệm thỏa mãn điều kiện \({t_1} \le 0 \le {t_2}\)
\(P \leqslant 0 \Leftrightarrow \dfrac{{3 – m}}{2} \leqslant 0 \Leftrightarrow m \geqslant 3\)
+ Phương trình (2) có hai nghiệm thỏa mãn điều kiện \(0 \le {t_1} \le {t_2}\)
\(\left\{ \matrix{ \Delta \ge 0 \hfill \cr S \ge 0 \hfill \cr P \ge 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ 1 – 8\left( {3 – m} \right) \ge 0 \hfill \cr – \dfrac{1 }{ 2} \ge 0 \hfill \cr \dfrac{3 – m}{ 2} \ge \hfill \cr} \right.\) . Không có m thỏa mãn các điều kiện này.
Vậy phương trình (1) có nghiệm khi \(m \ge 3\) .