Tóm tắt kiến thức và Giải bài 43, 44, 45, 46, 47 trang 27 SGK Toán 9 tập 1: Biến đổi đơn giản biểu thức chứa căn thức bậc hai.
1. Đưa thừa số ra ngoài dấu căn
Với hai biểu thức A, B mà B≥0, ta có √A2B = |A|√B tức là:
Nếu A ≥0 và B≥0 thì √A2B = A√B;
Nếu A<0 và B≥0 thì √A2B = -A√B.
2. Đưa thừa số vào trong dấu căn
Với A ≥0 và B≥0 thì A√B = √A2B
Với A<0 và B≥0 thì A√B = -√A2B
Hướng dẫn giải bài tập SGK trang 27 Toán 9 tập 1.
Bài 43. Viết các số hoặc biểu thức dấu căn thành dạng tích rồi đưa thừa số ra ngoài dấu căn:
a) √54;
b) √108;
c) 0,1√20000
d) -0,05√28800
e) √7.63.a2
Advertisements (Quảng cáo)
Giải: a) √54 = √9.6 = 3√6
b) √108 = √36.3 = 6√3
c) 0,1√20000 = 0,1√10000.2= 0,1.100√2 = 10√2
d) -0,05.√28800 = -0,05.√14400.2 = -0,05.120√2 = -6√2
e)√7.63.a2 = √7.7.9.a2 = 7.3|a| = 21|a|
Bài 44. Đưa thừa số vào trong dấu căn: 3√5; -5√2; -2/3√xy với xy ≥ 0; x√2/x với x > 0 và y ≥ 0.
Giải: 3√5 =√32.5 = √9.5 = 45
-5√2 =- √52.2 = -√50

Advertisements (Quảng cáo)

Bài 45 trang 27. So sánh:
a) 3√3 và √12
b) 7 và 3√5

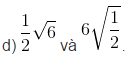
Giải: Đưa thừa số vào trong dấu căn rồi so sánh.
a) Ta có 3√3 = √27 vì 27 > 12 ⇒ √27 > √12 nên 3√3 > √12
b)3√5 = √9.5 = √45; 7= √49. Vì 49 > 45 nên 7 > 3√5

Bài 46. Rút gọn các biểu thức sau với x ≥ 0:
a) 2√3x – 4√3x + 27 – 3√3x
b) 3√2x – 5√8x + 7√18x + 28
Giải: a) 2√3x – 4√3x + 27 – 3√3x = 27 + (2-4-3 )√3x = 27 -5√3
Lưu ý. Các căn số bậc hai là những số thực. Do đó khó làm tính với căn số bậc hai, ta có thể vận dụng mọi quy tắc và mọi tính chất của các phép toàn trên số thực.
b) Dùng phép đưa thừa số ra ngoài dấu căn để có những căn thức giống nhau là √2x
3√2x – 5√8x + 7√18x + 28 = 3√2x – 5√4.2x + 7√9.2x + 28
=3√2x – 10√2x + 21√2x + 28 =28 + (3-10+21)√2x = 28 + 14√2x.
Bài 47 .

Giải a) Vì x ≥ 0, y ≥ 0 nên x + y ≥ 0. Do đó:
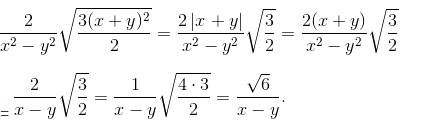 b)
b)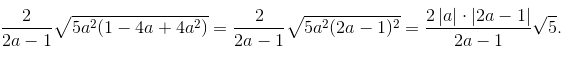
Vì a > 0,5 nên 2a – 1> 0. Do đó 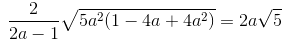




![[TX An Nhơn] thi học kì 2 lớp 9 môn Văn năm 2020: Tác phẩm “Những ngôi sao xa xôi” được Lê Minh Khuê viết vào năm nào?](https://dethikiemtra.com/wp-content/uploads/2020/06/canh-dong-100x75.jpg)

