Đề KSCL đầu năm lớp 9 toán năm 2015 trường THCS Kim Đồng

Đề và đáp án đề thi KSCL đầu năm lớp 9 Toán năm 2015 trường THCS Kim Đồng.

ĐỀ KHẢO SÁT CHẤT LƯỢNG ĐẦU NĂM TOÁN 9

(Thời gian làm bài 45 phút)

Bài 1 (4,5 điểm) Giải các phương trình sau:

a) 5(x – 2) = 3(x + 1)

c) |2x+7|=3

Bài 2 (2 điểm) Giải các bất phương trình sau:

a) (x + 2)² < (x – 1)(x + 1)

Bài 3 (3,5 điểm) Cho tam giác ABC vuông ở A, đường cao AH.

a) Chứng minh: ΔABC đồng dạng với Δ HBA

b) Cho AB = 6 cm, BC = 10 cm. Tính HB.

c) Vẽ HE ⊥ AB (E ∈ AB), HF ⊥ AC (F ∈ AC). Chứng minh: AE.AB = AF.AC.

---

ĐÁP ÁN VÀ BIỂU ĐIỂM TRƯỜNG THCS KIM ĐỒNG MÔN TOÁN LỚP 9

Bài 1 (4,5 điểm): Mỗi câu 1,5 điểm:

Câu a)	5(x – 2) = 3(x + 1) ⇔ 5x – 10 = 3x + 3⇔ 2x = 13 ⇔ x =13/2	1,5 đ
Câu b)	(ĐKXĐ: x ≠ – 1; x ≠ 2) ⇔ 2x(x – 2) + 3(x + 1) = 2(x + 1)(x – 2) ⇔ 2x2 – 4x  + 3x + 3 = 2(x2 – 2x + x – 2) ⇔ 2x2 – x  + 3 = 2x2 – 2x – 4 ⇔ x = – 7 (thoả mãn ĐKXĐ)	0,25 đ 0,5 đ 0,25 đ 0,25 đ 0,25 đ
Câu c)		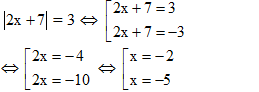1,5 đ

Bài 2 (2 điểm): Mỗi câu 1 điểm:

Câu a)	(x + 2)2 < (x – 1)(x + 1) ⇔x2 + 4x + 4 < x2 – 1 ⇔ 4x < – 5 ⇔x < –5/4	0,5 đ 0,5 đ
Câu b)		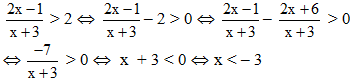0,5 đ 0,5 đ

Bài 3 (3,5 điểm) Cho tam giác ABC vuông ở A, đường cao AH.

Vẽ hình	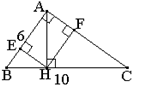(chưa cần vẽ HE và HF)	0,5 đ
Câu a)	Δ DABC  ∼ Δ DHBA: Chứng minh ΔABC   ∼  ΔHBA (g.g)	1 đ
Câu b)	Nêu được AB2 = BH.BC	0,5 đ 0,5 đ
Câu c)	Nêu được AH2 = AE.AB và AH2 = AF.BC ⇒ AE.AB = AF.AC.	0,5 đ 0,5 đ