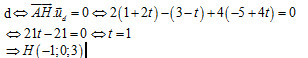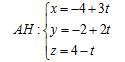Dưới đây là đề kiểm tra 1 tiết Hình học 12 chương 3 – THPT Phong Điền được Dethikiemtra.com cập nhật chi tiết. Các em cùng thử sức và so sánh kết quả với đáp án chi tiết bên dưới nhé.
ĐỀ KIỂM TRA 1 TIẾT
Môn: HÌNH HỌC 12 chương 3
Thời gian: 45 phút
1 (4,0đ): Cho ba điểm A(1,-2,0), B(-1,0,1), C(0,2,0)
a. (1,0đ) Chứng minh: A, B, C là ba đỉnh của một tam giác.
Advertisements (Quảng cáo)
b. (1,0đ) Xác định tọa độ điểm D sao cho ABCD là hình bình hành.
c. (1,0đ) Viết phương trình mặt phẳng (ABC).
Advertisements (Quảng cáo)
d. (1,0đ) Viết phương trình mặt cầu có đường kính AB.
2 (4,0đ): Cho điểm A(-4,-2,4) và
a) (2,0đ) Xác định tọa độ hình chiếu vuông góc của A trên đường thẳng d.
b) (2,0đ) Viết phương trình đường thẳng ∆ đi qua điểm A, cắt và vuông góc với đường thẳng d.
3 (2,0đ): Cho đường thẳng , mặt phẳng (P): x+y-2z+5 = 0 và điểm A(1,-1,2). Viết phương trình đường thẳng Δ cắt d và (P) lần lượt tại M và N sao cho A là trung điểm của đoạn MN.
ĐÁP ÁN ĐỀ KIỂM TRA 1 TIẾT HÌNH HỌC 12 CHƯƠNG 3 – THPT PHONG ĐIỀN
| Câu | Nội dung |
| 1 | a) A(1,-2,0), B(-1,0,1), C(0,2,0)
Ta có: vecto AC = (-1,4,0) vecto AB = (-2,2,1) Do 1/2 ≠ 4/2 ⇒ vecto AB và AC không cùng phương ⇔A, B, C không thẳng hàng (đ.p.c.m) |
| b) Gọi D(x,y,z) là điểm cần tìm.
Ta có: vecto AD = (x-1,y+2,z) Vecto BC – (1,2,-1)
Tứ giác ABCD là hình bình hành ⇔ vecto AD = BC |
|
| c) Ta có: vecto AC = (-1,4,0)
vecto AB = (-2,2,1)
Mặt phẳng (ABC) đi qua A(1,-2,0), và có 1 vtp là vecto n (ABC): 4(x-1) + (y+2) + 6(z-0) =0 ⇔ 4x+y+6z = 0 |
|
| d) Tâm I của mặt cầu cần tìm là trung điểm AB
⇒I (0,-1,1/2) Ta có: Bán kính mặt cầu là: R = AB/2 = 3/2 Vậy phương trình (S): x2 + (y+1)2 + (z-1/2)2 = 9/4 |
|
| 2 | a) Gọi H(-3+2t, 1-t, -1+4t) ∈ d ⇒ vecto AH = (1+2t, 3-t, -5+4t)
Đường thẳng d có 1 vectơ chỉ phương ud = (2, -1, 4) H là hình chiếu của A trên d
|
| b) Đường thẳng cần tìm là đường thẳng qua A(-4,-2,4) và có 1 vectơ chỉ phương AH = (3, 2, -1).
|
|
| 3 | Ta có: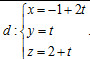 . Gọi M(-1+2t, t, 2+t) ∈ d . Gọi M(-1+2t, t, 2+t) ∈ d
Do A là trung điểm của MN, suy ra N(3-2t, -2-t, 2-t). Mặt khác: N ∈ (P) ⇔ 3-2t-2-t-2(2-t)+5 = 0 ⇔ t = 2 ⇒M(3,2,4). Đường thẳng đi qua A và M có phương trình: |