
Phần I: Trắc nghiệm (2đ)
Hãy chọn chữ cái đứng trước câu trả lời đúng cho các câu hỏi sau:
1. : Điều kiện để biểu thức\(A = \dfrac{{2017}}{{\sqrt x – 1}}\) xác định là:
A.\(x > 0\)
B.\(x > 1\)
C.\(x > 0,x \ne 1\)
D.\(x \ge 0,x \ne 1\)
2. (TH): Cho\(\sqrt {x – 1} = 2\), giá trị của \(x\) là:
A.\( – 3\) B.3
C.\( – 1\) D.5
3. : Cho biểu thức \(P = \sqrt {\dfrac{{5a}}{{32}}} .\sqrt {\dfrac{{2a}}{5}} \) với \(a \ge 0\), kết quả thu gọn của \(P\) là:
A.\(\dfrac{{\sqrt a }}{{16}}\). B.\(\dfrac{a}{4}\).
C.\(\dfrac{a}{{16}}\). D.\(\dfrac{{\sqrt a }}{4}\).
4. : Trong các hàm số dưới đây, hàm số bậc nhất có đồ thị đi qua điểm \(A\left( {1;4} \right)\)là:
A.\(y = {x^2} + 3\) B.\(y = x – 3\)
C.\(y = 4x\). D.\(y = 4 – x\).
5. : Cho 2 đường thẳng \(\left( {{d_1}} \right):y = \left( {{m^2} + 1} \right)x + 2\) và \(\left( {{d_2}} \right):y = 5x + m\). Hai đường thẳng đó trùng nhau khi:
A.\(m = \pm 2\) B.\(m = 2\)
C.\(m = – 2\) D.\(m \ne \pm 2\)
6. : Cho tam giác ABC vuông tại A. Trong các hệ thức sau, hệ thức đúng là:
A.\(\sin C = \dfrac{{BC}}{{AC}}\)
B.\(\cos C = \dfrac{{BC}}{{AC}}\)
C.\(\tan C = \dfrac{{AB}}{{AC}}\)
D.\(\cot C = \dfrac{{AB}}{{AC}}\)
7. : Cho hai điểm phân biệt A, B. Số đường thẳng đi qua hai điểm A, B là:
A.0 B.1
C.2 D.Vô số
|
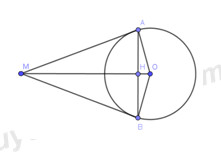
8. : Cho hình vẽ, MA và MB là hai tiếp tuyến của đường tròn \(\left( {O,3cm} \right)\), \(MA = 4cm\). Độ dài đoạn thẳng AB là: A.4,8cm B.2,4cm C.1,2cm D.9,6cm
|
 |
Phần II. Tự luận (8đ)
1. (2đ) Cho hai biểu thức \(A = \dfrac{{\sqrt x – 5}}{{\sqrt x }}\) và \(B = \dfrac{{\sqrt x }}{{\sqrt x – 5}} – \dfrac{{3\sqrt x }}{{x – 25}}\) với\(x > 0,x \ne 25\).
a) Tính giá trị biểu thức \(A\) khi\(x = 81\).
b) Cho\(P = A.B\), chứng minh rằng \(P = \dfrac{{\sqrt x + 2}}{{\sqrt x + 5}}\)
c) So sánh \(P\) và\({P^2}\).
2. (2đ) Cho hàm số \(y = \left( {m + 2} \right)x + 2{m^2} + 1\) (\(m\)là tham số)
a)Vẽ đồ thị hàm số trên khi\(m = – 1\).
b)Tìm \(m\)để hai đường thẳng \(\left( d \right)y = \left( {m + 2} \right)x + 2{m^2} + 1\)và \(\left( {d’} \right):y = 3x + 3\) cắt nhau tại một điểm trên trục tung.
3. (3,5đ) Cho đường tròn \(\left( O \right)\) đường kính AB và điểm C thuộc đường tròn \(\left( O \right)\)(C khác Avà B) sao cho\(AC > BC\). Qua O vẽ đường thẳng vuông góc với dây cung AC tại H. Tiếp tuyến tại Acủa đường tròn \(\left( O \right)\) cắt OHtại D. Đoạn thẳng DB cắt đường tròn \(\left( O \right)\) tại E.
a) Chứng minh \(HA = HC,\angle DCO = {90^o}\)
b) Chứng minh rằng \(DH.DO = DE.DB\)
Advertisements (Quảng cáo)
c) Trên tia đối của tia EA lấy điểm F sao cho Elà trung điểm cạnh AF. Từ F vẽ đường thẳng vuông góc với đường thẳng AD tại K. Đoạn thẳng FK cắt đường thẳng BC tại M. Chứng minh\(MK = MF\).
4. (0,5đ) Cho các số dương \(x,y\) thoả mãn\(x + y \le \dfrac{4}{3}\). Tìm giá trị nhỏ nhất của biểu thức
\(S = x + y + \dfrac{3}{{4x}} + \dfrac{3}{{4y}}\)

Phần I:
|
1D |
2D |
3B |
4C |
|
5B |
6C |
7B |
8A |
Phần II:
1. Cho hai biểu thức \(A = \dfrac{{\sqrt x – 5}}{{\sqrt x }}\) và \(B = \dfrac{{\sqrt x }}{{\sqrt x – 5}} – \dfrac{{3\sqrt x }}{{x – 25}}\) với\(x > 0,x \ne 25\).
a) Tính giá trị biểu thức \(A\) khi \(x = 81\).
Với\(x = 81\) ta có\(A = \dfrac{{\sqrt {81} – 5}}{{\sqrt {81} }} = \dfrac{{9 – 5}}{9} = \dfrac{4}{9}\).
Vậy với \(x = 81\) ta có\(A = \dfrac{4}{9}\).
b) Cho \(P = A.B\), chứng minh rằng \(P = \dfrac{{\sqrt x + 2}}{{\sqrt x + 5}}\)
\(\begin{array}{l}B = \dfrac{{\sqrt x }}{{\sqrt x – 5}} – \dfrac{{3\sqrt x }}{{x – 25}}\\\;\;\; = \dfrac{{\sqrt x \left( {\sqrt x + 5} \right)}}{{\left( {\sqrt x – 5} \right)\left( {\sqrt x + 5} \right)}} – \dfrac{{3\sqrt x }}{{\left( {\sqrt x – 5} \right)\left( {\sqrt x + 5} \right)}}\\\;\;\; = \dfrac{{x + 5\sqrt x – 3\sqrt x }}{{\left( {\sqrt x – 5} \right)\left( {\sqrt x + 5} \right)}} = \dfrac{{x – 2\sqrt x }}{{\left( {\sqrt x – 5} \right)\left( {\sqrt x + 5} \right)}}.\end{array}\)
Xét\(P = A.B = \dfrac{{\sqrt x – 5}}{{\sqrt x }}.\dfrac{{x + 2\sqrt x }}{{\left( {\sqrt x – 5} \right)\left( {\sqrt x + 5} \right)}} \)\(\;= \dfrac{{\sqrt x – 5}}{{\sqrt x }}.\dfrac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x + 5} \right)\left( {\sqrt x – 5} \right)}} \)\(\;= \dfrac{{\sqrt x + 2}}{{\sqrt x + 5}}\).
Vậy \(P = \dfrac{{\sqrt x + 2}}{{\sqrt x + 5}}\).\(\)
c) So sánh \(P\) và \({P^2}\).
Xét hiệu \(P – {P^2} = P\left( {1 – P} \right)\).
Nhận thấy: \(\left\{ \begin{array}{l}\sqrt x + 2 > 0\;\forall x > 0\\\sqrt x + 5 > 0\;\forall x > 0\end{array} \right. \Rightarrow \dfrac{{\sqrt x + 2}}{{\sqrt x + 5}} > 0\;\forall x > 0 \Rightarrow P > 0\;\forall x > 0\). (1)
Xét \(1 – P = 1 – \dfrac{{\sqrt x + 2}}{{\sqrt x + 5}} = \dfrac{{\sqrt x + 5 – \left( {\sqrt x + 2} \right)}}{{\sqrt x + 5}} = \dfrac{3}{{\sqrt x + 5}}\).
Vì \(\sqrt x + 5 > 0\;\forall x > 0\)
\(\Rightarrow \dfrac{3}{{\sqrt x + 5}} > 0\;\forall x > 0 \Rightarrow 1 – P > 0\;\forall x > 0\). (2)
Từ (1) và (2) \( \Rightarrow P\left( {1 – P} \right) > 0\;\forall x > 0 \Rightarrow P – {P^2} > 0\;\forall x > 0 \Rightarrow P > {P^2}\;\forall x > 0\).
Vậy \(P > {P^2}\) với mọi x thỏa mãnĐKXĐ.
2. Cho hàm số \(y = \left( {m + 2} \right)x + 2{m^2} + 1\) (\(m\)là tham số)
a) Vẽ đồ thị hàm số trên khi\(m = – 1\).
Advertisements (Quảng cáo)
Với \(m = – 1\) ta có hàm số có dạng:\(y = x + 3\)
Chọn\(x = 0 \Rightarrow y = 3 \Rightarrow \)\(A\left( {0;3} \right)\)thuộc đồ thị hàm số
Chọn\(y = 0 \Rightarrow x + 3 = 0 \Leftrightarrow x = – 3 \Rightarrow B\left( { – 3;\;0} \right)\) thuộc đồ thị hàm số.
Từ đó ta có đồ thị hàm số:
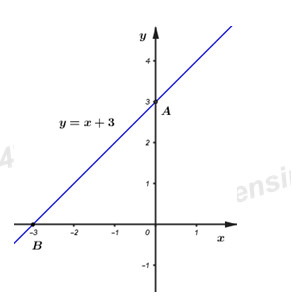
b)Tìm \(m\)để hai đường thẳng \(\left( d \right)y = \left( {m + 2} \right)x + 2{m^2} + 1\)và \(\left( {d’} \right):y = 3x + 3\) cắt nhau tại một điểm trên trục tung.
Phương trình của trục tung có dạng \(x = 0\). Thay \(x = 0\) vào hàm số \(\left( {d’} \right):y = 3x + 3\) ta có \(y = 3\)
Suy ra \(A\left( {0;3} \right)\) là giao điểm của\(\left( {d’} \right):y = 3x + 3\) và trục tung.
Vì hai đường thẳng \(\left( d \right):y = \left( {m + 2} \right)x + 2{m^2} + 1\)và \(\left( {d’} \right):y = 3x + 3\) cắt nhau tại một điểm trên trục tung nên điểm \(A\left( {0;3} \right)\) thuộc đường thẳng \(\left( d \right):y = \left( {m + 2} \right)x + 2{m^2} + 1\)
\( \Rightarrow 3 = \left( {m + 2} \right).0 + 2{m^2} + 1 \Leftrightarrow {m^2} = 1 \Leftrightarrow m = \pm 1\).
Với \(m = 1 \Rightarrow y = 3x + 3 \Rightarrow \)\(\left( d \right)\) trùng với \(\left( {d’} \right):y = 3x + 3\) (loại vì nếu hai đường thẳng trùng nhau thì không thể cắt nhau tại 1đ)
Với \(m = – 1 \Rightarrow y = x + 3\) (thỏa mãn)
Vậy\(m = – 1\) là giá trị cần tìm.
3. Cho đường tròn \(\left( O \right)\) đường kính AB và điểm C thuộc đường tròn \(\left( O \right)\)(C khác Avà B) sao cho\(AC > BC\). Qua O vẽ đường thẳng vuông góc với dây cung AC tại H. Tiếp tuyến tại A của đường tròn \(\left( O \right)\) cắt OH tại D. Đoạn thẳng DB cắt đường tròn \(\left( O \right)\) tại E.
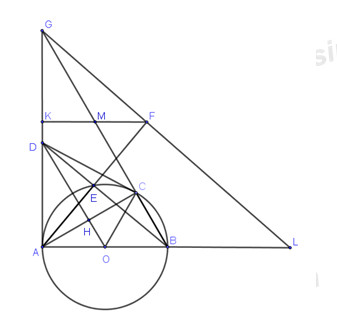
a)Chứng minh \(HA = HC,\angle DCO = {90^o}\)
Xét tam giác AOC có: \(AO = CO\)(do cùng là bán kính), suy ra tam giác AOC cân tại O
Mà có OH là đường cao ứng với đỉnh O nên OH đồng thời cũng là trung trực của AC
Suy ra \(HA = HC\). (đpcm)
Xét tam giác AOC cân tại O có OH là đường cao, suy ra OH đồng thời là đường phân giác
\( \Rightarrow \angle AOH = \angle COH\).
Xét tam giác DOC và tam giác DOA có:
+) Chung cạnh OD
+) \(AO = CO\)(do cùng là bán kính)
+) \(\angle AOH = \angle COH\)
\( \Rightarrow \Delta DOC = \Delta DOA \Rightarrow \angle DCO = \angle DAO = {90^o}\)(do AD là tiếp tuyến nên \(\angle DAO = {90^o}\))\(\)\(\)
b)Chứng minh rằng \(DH.DO = DE.DB\)
Xét tam giác vuông ADO vuông tại A có AHlà đường cao
\( \Rightarrow A{D^2} = DH.DO\) (hệ thức lượng trong tam giác vuông) (1)
Xét tam giác vuông DABvuông tại A có AElà đường cao ( AE vuông góc với BD do \(\angle AEB\)là góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow A{D^2} = DE.DB\) (hệ thức lượng trong tam giác vuông) (2)
Từ (1) và (2) suy ra \(DH.DO = DE.DB\;\;\left( { = A{D^2}} \right)\) (đpcm) \(\)\(\)
c) Trên tia đối của tia EA lấy điểm F sao cho Elà trung điểm cạnh AF. Từ F vẽ đường thẳng vuông góc với đường thẳng AD tại K. Đoạn thẳng FKcắt đường thẳng BC tại M. Chứng minh\(MK = MF\).
Kéo dài BM cắt AD tại G, GF cắt AB tại L
Xét tam giác ABG có:
\(\begin{array}{l}DO//BG\;\left( { \bot AC} \right)\\OA = OB\;\left( { = R} \right)\end{array}\)
\( \Rightarrow AD = DG\) (tính chất đường trung bình)
Xét tam giác GFA có:
+) D là trung điểm củaAG (do\(AD = DG\))
+)E là trung điểm của AF (giả thiết)
\( \Rightarrow \)DE song song với GF(tính chất đường trung bình)
Xét tam giác GAL có:
+) D là trung điểm AG (do \(AD = DG\))
+) DB song song với GL (do DE song song với GF)
Suy ra B là trung điểm của AL (tính chất đường trung bình), suy ra\(AB = \dfrac{1}{2}AL\)\(\)
Xét tam giác GKM có KM song song với AB (do cùng vuông góc với AG)
\( \Rightarrow \dfrac{{KM}}{{AB}} = \dfrac{{KG}}{{AG}}\) (định lí Ta-lét) (3)
Xét tam giác GAL có KF song song với AL (do cùng vuông góc với AG)
\( \Rightarrow \dfrac{{KF}}{{AL}} = \dfrac{{GK}}{{AG}}\) (định lí Ta-lét) (4)
Từ (3) và (4) \( \Rightarrow \dfrac{{KM}}{{AB}} = \dfrac{{KF}}{{AL}}\). Mà có \(AB = \dfrac{1}{2}AL\) (cmt)
\( \Rightarrow KM = \dfrac{1}{2}KF \Rightarrow MF = KF – KM = KF – \dfrac{1}{2}KF = \dfrac{1}{2}KF \Rightarrow KF = KM\)(đpcm).
4. Cho các số dương \(x,y\) thoả mãn\(x + y \le \dfrac{4}{3}\). Tìm giá trị nhỏ nhất của biểu thức\(S = x + y + \dfrac{3}{{4x}} + \dfrac{3}{{4y}}\)
Ta có: \(S = \left( {x + \dfrac{4}{{9x}}} \right) + \left( {y + \dfrac{4}{{9y}}} \right) + \dfrac{{11}}{{36}}\left( {\dfrac{1}{x} + \dfrac{1}{y}} \right)\).
Áp dụng bất đẳng thức Co-si có:
\(\begin{array}{l} + )\;x + \dfrac{4}{{9x}} \ge 2\sqrt {x.\dfrac{4}{{9x}}} = 2.\sqrt {\dfrac{4}{9}} = \dfrac{4}{3}\\ + )\;y + \dfrac{4}{{9y}} \ge 2\sqrt {y.\dfrac{4}{{9y}}} = 2\sqrt {\dfrac{4}{9}} = \dfrac{4}{3}\end{array}\)
Chứng minh bất đẳng thức phụ:
\(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}} \Leftrightarrow \dfrac{{x + y}}{{xy}} \ge \dfrac{4}{{x + y}} \Leftrightarrow {\left( {x + y} \right)^2} \ge 4xy \Leftrightarrow {\left( {x – y} \right)^2} \ge 0\)(luôn đúng)
Áp dụng bất đẳng thức phụ trên có: \(\dfrac{{11}}{{36}}\left( {\dfrac{1}{x} + \dfrac{1}{y}} \right) \ge \dfrac{{11}}{{36}}.\dfrac{4}{{x + y}}\)
Mà có \(x + y \le \dfrac{4}{3} \Rightarrow \dfrac{{11}}{{36}}.\left( {\dfrac{1}{x} + \dfrac{1}{y}} \right) \ge \dfrac{{11}}{{36}}.\dfrac{4}{{x + y}} \ge \dfrac{{11}}{{36}}.\dfrac{4}{{\dfrac{4}{3}}} = \dfrac{{11}}{{12}}\).
\( \Rightarrow S = \left( {x + \dfrac{4}{{9x}}} \right) + \left( {y + \dfrac{4}{{9y}}} \right) + \dfrac{{11}}{{36}}\left( {\dfrac{1}{x} + \dfrac{1}{y}} \right) \ge \dfrac{4}{3} + \dfrac{4}{3} + \dfrac{{11}}{{12}} = \dfrac{{43}}{{12}}\).
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{4}{{9x}}\\y = \dfrac{4}{{9y}}\\x + y = \dfrac{4}{3}\\x = y\end{array} \right. \Leftrightarrow x = y = \dfrac{2}{3}\)
Vậy giá trị nhỏ nhất của biểu thức là \(\dfrac{{43}}{{12}}\) khi\(x = y = \dfrac{2}{3}\).





