Chia sẻ đề kiểm tra Toán lớp 9 15 phút Chương 3 Đại số: Xác định một phương trình bậc nhất hai ẩn số, biết hai nghiệm là ( 3; 5) và ( 0; −2)

Bài 1: Viết công thức nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của phương trình : \(2x + 0.y = 4.\)

Bài 2: Xác định một phương trình bậc nhất hai ẩn số, biết hai nghiệm là \(( 3; 5)\) và \(( 0; −2)\).

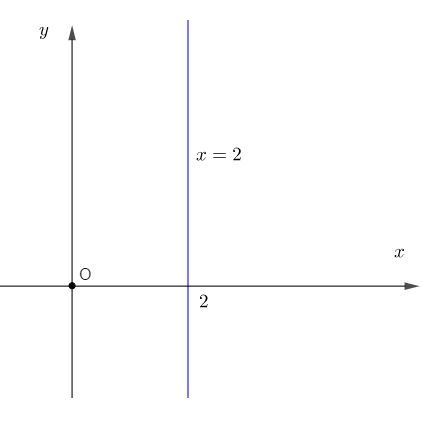
Bài 1:Ta có : \(x = 2.\)

Công thức  nghiệm tổng quát : \((2; y)\); y tùy ý.

Đường thẳng \(x = 2\) song song với Oy cắt Ox tại điểm có hoành độ bằng 2 ( xem hình vẽ).

Bài 2: Phương trình có dạng : \(ax + by = c.\)

Nếu \(a = 0\), b khác 0, ta có : \(by = c.\)

( 3; 5) và ( 0; −2) là nghiệm \( \Rightarrow {c \over b} = 5\) và \({c \over b} =  – 2\) ( vô nghiệm).

Nếu a khác 0; \(b = 0\), ta có : \(ax = c.\)

Tương tự : \({c \over a} = 3\) và \({c \over a} = 0\) ( vô nghiệm).

Nếu a khác 0 và b khác 0, ta đưa về bài toán viết phương trình đường thẳng (d) : y = mx + n qua

hai điểm \(( 3; 5)\) và \(( 0; −2)\).

Điểm \((0; −2)\) thuộc (d) \(=> n = −2.\) Khi đó : \(y = mx – 2.\)

Điểm \(( 3; 5)\) thuộc (d) => \(m = {7 \over 3}\)

Vậy : \(y = {7 \over 3}x – 2 \Leftrightarrow 7x – 3y – 6 = 0.\)