Đáp án và hướng dẫn Giải bài 44, 45, 46, 47 trang 86; Bài 48, 49, 50, 51, 52 trang 87 SGK Toán 9 tập 2: Cung chứa góc – Chương 3 hình học.
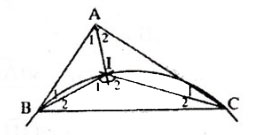
Bài 44. Cho ΔABC vuông ở A, có cạnh BC cố định. Gọi I là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm I khi A thay đổi.
 bai44
bai44
Theo tính chất của góc ngoài tam giác, ta có:
∠I1=∠A1 + ∠B1 (1)
∠I2=∠A2 + ∠C1 (2)
Cộng vế (1) và (2) vế với vế:
∠I1 + ∠I2 = ∠A1 + ∠B1 + ∠A2 + ∠C1
Hay ∠I = 900 + 450 =1350
Điểm I nhìn đoạn-thẳng BC cố định dưới góc 1350 không đổi, vậy quỹ tích của I là góc cung-chứa-góc 1350 dựng trên đoạn-thẳng BC
 bai45
bai45
Bài 45. Cho các hình thoi ABCD có cạnh AB cố định. Tìm quỹ tích giao điểm O của hai đường chéo của các hình thoi đó.
Theo tính chất của hình thoi, các đường chéo hình thoi vuông góc với nhau. Như vậy nếu cạnh AB cố định giao điểm O của các đường chéo hình thoi ABCD dưới góc 900 không đổi. Vậy quỹ tích giao điểm O của hai đường chéo hình thoi ABCD khi AB cố định là đườngtròn đường kính AB.
Bài 46 trang 86. Dựng một cung-chứa-góc 55o trên đoạn thẳng AB = 3cm
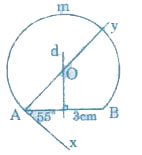
Trình tự dựng như sau:
– Dựng đoạnthẳng AB = 3cm (dùng thước đo chia khoảng mm)
– Dựng góc xAB = 55o (dùng thước đo góc và thước thẳng)
– Dựng tia Ay vuông góc với Ax (dùng êke)
– Dựng đường trung trực d của đoạnthẳng AB (dùng thước có chi khoảng và êke). Gọi O là giao điểm của d và Ay.
– Dựng đườngtròn tâm O, bán kính OA (dùng compa)
Ta có: Cung AmB là cung-chứa-góc 550 dựng trên đoạnthẳng AB = 3cm (một cung)
Bài 47 trang 86. Gọi cung chứagóc 55o ở bài tập 46 là cung AmB. Lấy điểm M1 nằm bên trong và điểm M2 nằm bên ngoài đườngtròn chứa cung này sao cho M1, M2 và cung AmB nằm cùng về một phía đối với đường thẳng AB. Chứng minh rằng:
a) ∠AM1B > 550;
b) ∠AM2B < 550.
 bai47
bai47
Advertisements (Quảng cáo)
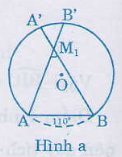
a)
M1 là điểm bất kì nằm trong cung chứagóc 550 (hình a). Gọi B’, A’ theo thứ tự là giao điểm của M1A, M1B với cung tròn. Vì ∠AM1B là góc có đỉnh nằm trong đường -tròn, nên:
∠AM1B = sđ cung(AB +A’B’)/2 = sđcung AB/2 + sđcung A’B’/2 = 550+ (một số dương)
Vậy ∠AM1B > 550
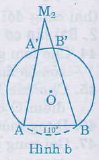
b)
 bai47b
bai47b
M2 là điểm bất kì nằm ngoài đườngtròn (h.b), M2A, M2B lần lượt cắt đườngtròn tại A’, B’. Vì ∠AM2B là góc có đỉnh nằm bên ngoài đườngtròn nên: ∠AM2B= sđcung(AB – A’B’)/2= sđAB/2 – sđA’B’/2 = 550 – (một số dương)
Vậy ∠AM2B < 550
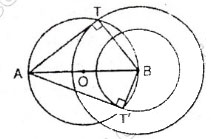
Bài 48 trang 87 Toán 9 tập 2 . Cho hai điểm A, B cố định. Từ A vẽ các tiếp tuyến với đường tròn tâm B bán kính không lớn hơn AB. Tìm quỹ tích các tiếp điểm.
 bai48
bai48
Trường hợp các đường-tròn tâm B có bán kính nhỏ hơn BA. Giả sử AT là tiếp tuyến của đường-tròn tâm B. Với T là tiếp điểm.
Khi đó AT⊥BT ⇒ ∠ATB = 900. Điểm T nhìn đoạn AB cố định dưới một góc vuông nnê quỹ tích của T là đường-tròn đường kính AB.
– Trường hợp đường-tròn tâm B, có bán kính bằng BA. Khi oó quỹ tích chỉ là điểm A.
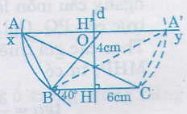
Bài 49 trang 87. Dựng ΔABC, biết BC = 6cm, ∠A = 40o và đường cao AH = 4cm.
Trình tự dựng gồm 3 bước:
– Dựng đoạn-thẳng BC = 6cm
– Dựng cungchứagóc 40o trên đoạn-thẳng BC.
Advertisements (Quảng cáo)
– Dựng đường thẳng xy song song với BC và cách BC một khoảng là 4cm như sau:
Trên đường trung trực d của đoạnthẳng BC lấy đoạn HH’ = 4cm (dùng thước có chia khoảng mm). Dựng đường thẳng xy vuông góc với HH’ tại H
Gọi giao điểm xy và cungchứagóc là ∠A, ∠A’. Khi đó ΔABC hoặc A’BC đều thỏa yêu cầu của đề toán.
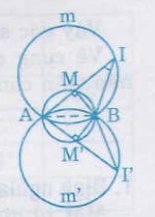
Bài 50. Cho đườngtròn đường-kính AB cố định. M là một điểm chạy trên đườngtròn. Trên tia đối của tia MA lấy điểm I sao cho MI = 2MB.
a) Chứng minh ∠AIB không đổi.
b) Tìm tập hợp các điểm I nói trên.
 bai50
bai50
Đáp án.
a)
Vì ∠BMA = 900 (góc nội tiếp chắn nửa đgtròn) suy ra trong Δvuông MIB có tg∠AIB = MB/MI = 1/2
⇒ ∠AIB = 26034’
Vậy ∠AIB không đổi.
b) Phần thuận:
Khi điểm M chuyển động trên đgtròn đường-kính AB thì điểm I cũng chuyển động, nhưng luôn nhìn đoạn-thẳng AB cố định dưới góc 26o34’, vậy điểm I thuộc hai cung chứagóc 26o34’ dựng trên đoạn thẳng AB (hai cung AmB và Am’B)
Phần đảo:
Lấy điểm I’ bất kì thuộc cung AmB hoặc cung Am’B, I’A cắt đgtròn đườngkính AB tại M’.
Δvuông BMT, có tg∠I’ = M’B/M’I’ = tg26034’
Kết luận: Quỹ tích điểm I là hai cung cung AmB và Am’B.
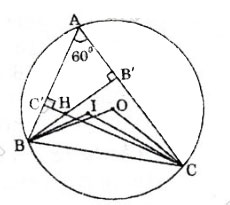
Bài 51. Cho I, O lần lượt là tâm đgtròn nội tiếp, tâm đường tròn ngoại tiếp ΔABC với ∠A = 600. Gọi H là giao điểm của các đường cao BB’ và CC’
Chứng minh các điểm B, C, O, H, I cùng thuộc một đgtròn.
 bai51
bai51
Xét tứ giác AB’HC’ ta có:
∠B’HC’ = 3600 -(∠A +∠B’ + ∠C’)
=3600 – (600 + 900 + 900) = 1200
⇒ ∠BHC =1200 (Đối đỉnh với góc B’HC’)
Trong ΔBIC ta có:
∠BIC = 1800 – (∠IBC + ∠ICB) = 1800 -(∠B/2 + ∠C/2)
=1800 -1/2(1800 -∠A) =1800 -1/2(1800 – 600) =1200
Như vậy H, I đều nằm trên cung chứagóc 1200 dựng trên BC.Mặt khác ΔABC nội tiếp trong đường–tròn tâm O nên góc nội tiếp BAC trong đường tròn (O) có số đo:
600 = ∠BAC =1/2sđ cungBC =1/2 ∠BOC ⇒∠BOC =1200
Vậy O cùng nằm trên cungchứagóc 1200 dựng trên BC. ĐIều này có nghĩa là 5 điểm B,C,O,H,I nằm trên cùng một đườngtròn chứa cung-chứa-góc 1200 dựng trên BC.
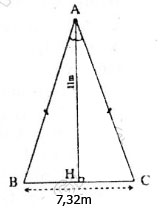
Bài 52. “Góc sút” của quả phạt đền 11 mét là bao nhiêu độ? Biết rằng chiều rộng cầu môn là 7,32m. Hãy chỉ ra hai vị trí khác trên sân có cùng “góc sút” như quả phạt đền 11 m.
 bai52
bai52
Gọi BC là bề rộng của cầu môn BC =7,32m
Bóng dặt ở vị trí A sao cho ΔABC cân tại A có đường cao AH =11m thì “góc sút” là góc BAC.
Ta có: ΔABC cân tại A.
⇒ HB =HC =3,66m (đường cao AH cũng là trung tuyến)
ΔAHB vuông ở H.
⇒tg∠A1 = BH/AH=3,66/11=0,3327
⇒∠A1 ≈ 18040′ ⇒ ∠BAC ≈2.18040’=37020′
Do đó góc sút của quả phạt đền là: 37020′
Điểm A nhìn BC dưới một góc 37020′ dựng trên đoạn BC.

![[THCS Bình Giang] kiểm tra môn Sử lớp 9: Em hãy trình bày ngắn gọn diễn biến, kết quả của chiến dịch lịch sử Điện Biên Phủ năm 1954?](https://dethikiemtra.com/wp-content/uploads/2019/03/dongphongnha-100x75.jpg)




