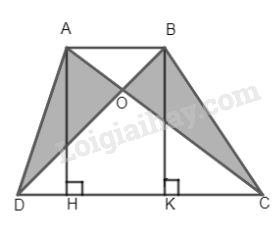
Cho hình thang ABCD \(\left( {AB//CD} \right)\). Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh rằng: \({S_{AOD}} = {S_{BOC}}.\) … trong Kiểm tra Toán lớp 8 15 phút Chương 2 Hình học 8. Xem Đề và đáp án đầy đủ phía dưới đây

Cho hình thang ABCD \(\left( {AB//CD} \right)\). Gọi O là giao điểm của hai đường chéo AC và BD.
a) Chứng minh rằng: \({S_{AOD}} = {S_{BOC}}.\)
b) Gọi M là trung điểm của BC. Từ M kẻ đường thẳng song song với AD cắt AB tại E và DC tại F.
Chứng minh rằng: \({S_{ABCD}} = {S_{AEFD}}.\)

a)
Advertisements (Quảng cáo)
Ta có \({S_{ADC}} = {S_{DBC}}\) (chung đáy DC và đường cao AH = BK)
\( \Rightarrow {S_{ADC}} – {S_{DOC}} = {S_{DBC}} – {S_{DOC}}\)
Hay \({S_{AOD}} = {S_{BOC}}.\)
b)
Advertisements (Quảng cáo)
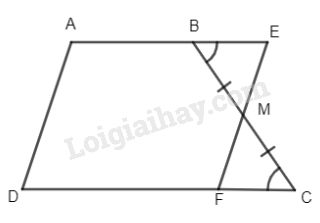
Ta có: \(\Delta BME = \Delta CMF(g.c.g)\)
\( \Rightarrow {S_{BME}} = {S_{CMF}}\)
\( \Rightarrow {S_{BME}} + {S_{ABMFD}} = {S_{CMF}} + {S_{ABMFD}}\)
Hay \({S_{AEFD}} = {S_{ABCD}}.\)




![[THCS Tân Viên] thi học kì 2 lớp 8 môn Địa: Hãy vẽ biểu đồ hình tròn thể hiện cơ cấu diện tích của ba nhóm đất chính của nước ta](https://dethikiemtra.com/wp-content/uploads/2020/09/anhbaitren13-100x75.jpg)

