Làm tính chia: \(\left( {3{x^5} – 5{x^4} – 3x + 1} \right):\left( {{x^2} – x – 1} \right)\) … trong Kiểm tra 15 phút Toán Chương 1 Đại số 8. Xem Đề và đáp án đầy đủ phía dưới đây

Bài 1. Làm tính chia:
a) \(\left( {3{x^5} – 5{x^4} – 3x + 1} \right):\left( {{x^2} – x – 1} \right)\)
b) \(\left( {{x^4} – 1} \right):\left( {x – 1} \right)\)

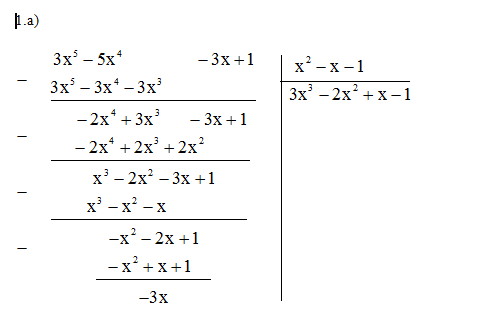
Advertisements (Quảng cáo)
Vậy \(3{x^5} – 5{x^4} – 3x + 1 \)\(\;= \left( {{x^2} – x – 1} \right)\left( {3{x^3} – 2{x^2} + x – 1} \right) – 3x.\)
b) Ta có: \({x^4} – 1 = \left( {{x^2} – 1} \right)\left( {{x^2} + 1} \right) \)\(\;= \left( {x – 1} \right)\left( {x + 1} \right)\left( {{x^2} + 1} \right)\)
Vậy \(\left( {{x^4} – 1} \right):\left( {x – 1} \right)\) , ta được thương là đa thức:
Advertisements (Quảng cáo)
\(\left( {x + 1} \right)\left( {{x^2} + 1} \right) = {x^3} + {x^2} + x + 1.\)

![[Phòng GD An Biên] kiểm tra cuối năm lớp 8 môn GDCD: So sánh điểm giống nhau và khác nhau giữa quyền khiếu nại với quyền tố cáo](https://dethikiemtra.com/wp-content/uploads/2020/09/bo-suu-tap-tranh-ve-co-giao-va-hoc-sinh-1-100x75.jpg)



