Kiểm tra 15 phút môn Toán – Chương 1 Hình học 8: Chứng minh rằng M và N đối xứng với nhau qua O

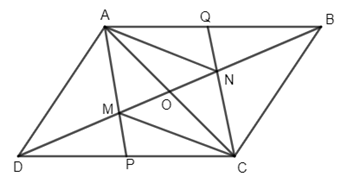
Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho DM = MN = NB. Gọi O là giao điểm của hai đường chéo AC và BD.

a)Chứng minh rằng M và N đối xứng với nhau qua O.

b)Gọi P, Q lần lượt là giao điểm của AM và CN với các cạnh DC và AB. Chứng minh rằng P và Q đối xứng nhau qua O.

a) Ta có: OB = OD (tính chất hai đường chéo của hình bình hành)

 BN = DM (gt)

\( \Rightarrow OB – BN = OD – DM\)

\( \Rightarrow ON = OM\) hay O là trung điểm MN chứng tỏ M và N đối xứng nhau qua O.

b) Tứ giác ANCM có OM = ON (cmt)

                        OA = OC (gt)

\( \Rightarrow ANCM\) là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường) \( \Rightarrow AM// CN\) hay \(AP// CQ\) lại có \(AQ//CP.\) Do đó AQCP là hình bình hành (các cạnh đối song song) mà O là trung điểm của đường chéo AC nên đường chéo thứ hai PQ phải qua O hay OP = OQ.

Chứng tỏ P và Q đối xứng nhau qua O.