Cho hình chữ nhật ABCD, từ M bất kì trên AB, kẻ đường thẳng song song với BC cắt CD tại N và đường chéo BD tại I … trong Đề kiểm tra môn Toán 15 phút Chương 2 Hình học 8.Xem Đề và đáp án đầy đủ phía dưới đây

Cho hình chữ nhật ABCD, từ M bất kì trên AB, kẻ đường thẳng song song với BC cắt CD tại N và đường chéo BD tại I. Qua I kẻ đường thẳng song song với AB cắt hai cạnh BC và AD lần lượt tại P và Q. Chứng minh rằng hai hình chữ nhật MIQA và NIPC có cùng diện tích

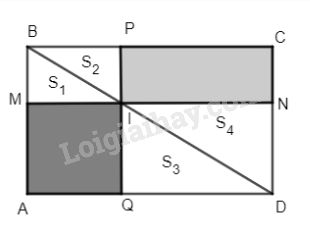
Ta có \(\Delta ABD = \Delta CDB\left( {c.g.c} \right)\)
Advertisements (Quảng cáo)
\( \Rightarrow {S_{ABD}} = {S_{CBD}}\left( {c.g.c} \right)\)
Tương tự \({S_1} = {S_2},{S_3} = {S_4}.\)
Advertisements (Quảng cáo)
Do đó: \({S_{ABD}} – \left( {{S_1} + {S_2}} \right) = {S_{CDB}} – \left( {{S_1} + {S_4}} \right)\)
Hay \({S_{MIQA}} = {S_{NIPC}}.\)