
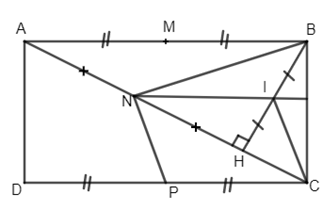
Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ B xuống AC. Gọi M, N, P lần lượt là trung điểm của AB, AH và DC.
a)Chứng minh MBCP là hình chữ nhật.
b)Chứng minh \(BN \bot NP.\)

Advertisements (Quảng cáo)
a) M, P lần lượt là trung điểm của AB và CD mà \(AB// CD\) và \(AB = CD\left( {gt} \right)\)
\( \Rightarrow MB//CP\) và MB = CP. Do đó MBCP là hình bình hành lại có \(\widehat {MBC} = {90^ \circ }\) nên MBCP là hình chữ nhật.
b) Gọi I là trung điểm của BH. Ta có NI là đường trung bình của \(\Delta AHB\) (vì N là trung điểm của AH)
Advertisements (Quảng cáo)
\( \Rightarrow NI// AB\) và \(NI = \dfrac{1 }{ 2}AB\) mà AB = CD và P là trung điểm của BC nên \(NI// CP\) và \(NI = CP.\)
Do đó NICP là hình bình hành \( \Rightarrow PN// CI\) mà I là trực tâm \(\Delta BNC\) \( \Rightarrow CI \bot BN.\)
Do đó \(BN \bot PN.\)





