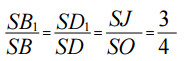Đề kiểm tra 1 tiết Hình học lớp 11 chương 2 có đáp án chi tiết đã được Dethikiemtra. com cập nhật chi tiết.
BÀI KIỂM TRA HÌNH HỌC CHƯƠNG 2 – LỚP 11 .
A. PHẦN TRẮC NGHIỆM
1: Trong các mệnh đề sau, mệnh đề nào đúng?
(A) Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
(B) Hai đgthẳng không có điểm chung thì chéo nhau
(C) Hai đg thẳng chéo nhau thì không có điểm chung
(D) Hai đườngthẳng phân biệt không // thì chéo nhau
2: Cho tam giác ABC. Trên cạnh AC kéo dài về phía A ta lấy một điểm D. Các mệnh đề nào sau đây sai?
(A) D ∈ (ABC)
(B) A ∈(ABC)
(C) (ABC) = (DBC)
(D) BD ∉ (ABC)
3: Cho các giả thiết sau đây. Giả thiết nào kết luận đườngthẳng a // với mặt phẳng (α) ?
A) a // b và b // (α)
(B) a ∩ (α) = 0
(C) a // b và b ⊂ (α)
(D) a // (β) và (α) // (β)
4: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC. G là trọng tâm tam giác BCD. Khi ấy, giao điểm của đườngthẳng MG và mặt phẳng(ABC) là: (A) Điểm C
(B) Giao điểm MG và AN
(C) Điểm N
(D) Giao điểm của MG và BC.
5: Cho hình lăng trụ tam giác ABC A’B’C’. Gọi I; J lần lượt là trọng tâm các tam giác ABC và A’B’C’. Thiết diện tạo bởi mp (AIJ) với lăng trụ đã cho là:
Advertisements (Quảng cáo)
(A) Tam giác cân
(B) Tam giác vuông
(C) Hình thang
(D) Hình bình hành
6: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Giao tuyến của hai mp(SAD) và (SBC) là đường.thẳng // với đườngthẳng nào sau đây?
(A) AC (B) BD (C) AD (D) SC
7: Cho tứ diện ABCD. Gọi G, E lần lượt là trọng tâm của các tam giác ABD và ABC. Mệnh đề nào sau đây đúng?
(A) GE // với CD
(B) GE cắt CD
(C) GE và CD chéo nhau
(D) GE cắt AD
8: Cho hình chóp S.ABCD. Gọi AC ∩ BD = I; AB ∩ CD = J; AD ∩ BC = K; Đẳng thức nào sai trong các đẳng thức sau đây?
(A) (SAC) ∩ (SBD) = SI
(B) (SAB) ∩ (SCD) = SJ.
Advertisements (Quảng cáo)
(C) (SAD) ∩ (SBC) = SK
(D) (SAC) ∩ (SAD) =AB.
9: Cho tứ diện ABCD. Gọi I, J, K lần lượt là trung điểm của AC, BC và BD. Giao tuyến của hai mặt phẳng (ABD) và (IJK) là:
(A) KD
(B) KI.
(C) Đường.thẳng qua K và song song với AB
(D) Không có.
10: Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt. Kết quả nào sau đây đúng?
(A) AD // (BEF)
(B) (AFD) // (BCE)
(C) (ABD) // (EFC)
(D) EC // (ABF).
11: Trong các mệnh đề sau; mệnh đề nào đúng?
(A) Hình chiếu // của hai đg thẳng chéo nhau thì // với nhau.
(B) Hình chiếu // của hai đg thẳng cắt nhau có thể // với nhau.
(C) Hình chiếu // của hai đgthẳng chéo nhau có thể // với nhau.
(D) Các mệnh đề trên sai.
12: Cho tứ diện ABCD cạnh bằng a. Gọi G là trọng tâm Δ ABC. Cắt tứ diện bởi mp (GCD) thì diện tích thiết diện là:

B – PHẦN TỰ LUẬN:
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. M, N, P lần lượt là trung điểm các cạnh AB, AD, SC.
(A) Tìm thiết diện của hình chóp S.ABCD và mp (MNP).
(B) Giả sử mp (MNP) cắt SB; SD lần lượt tại B1, D1. Chứng minh B1D1 // mp (ABCD).
(C) Tính SB/SB1 và SD/SD1 ?
KẾT QUAT ĐỀ KIỂM TRA 1 TIẾT HÌNH HỌC 11 CHƯƠNG 2
| Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Kết quả | C | D | B | B | D | C | A | D | C | B | C | B |
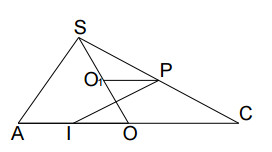
Gọi O = AC ∩ BD
I = MN ∩ AC
J = IP ∩ SO
Kẻ PO1// OC ⇒ PO1= OC/2
Mặt khác: OI = OC/2 ⇒ PO1= OI
⇒ OJ = JO1
và SO1= O1O hay OJ = 1/4SO
Mà B1D1 // BD và B1D1 qua J nên: