A. PHẦN TRẮC NGHIỆM: (4đ)
1. : Cho hình bình hành \(ABCD\). Trong các khẳng định sau hãy tìm khẳng định sai ?
A. \(\overrightarrow {AB} = \overrightarrow {DC} \).
B. \(\left| {\overrightarrow {AD} } \right| = \left| {\overrightarrow {CB} } \right|\).
C. \(\overrightarrow {AD} = \overrightarrow {CB} \).
D. \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\).
2. : Tìm tọa độ đỉnh parabol \(y = – 2{x^2} + 4x – 2\).
A. \(I\left( {1;1} \right)\). B. \(I\left( { – 2;2} \right)\).
C. \(I\left( {1;0} \right)\). D. \(I\left( {2;2} \right)\).
3. : Trong mặt phẳng tọa độ Oxy cho hai vectơ \(\overrightarrow a = (1;2),\,\overrightarrow {\,\,\,b} = ( – 3;5).\,\)Tìm tọa độ của vectơ \(\overrightarrow u = \overrightarrow a – \overrightarrow b .\)
A. \(\overrightarrow u = ( – 4;3).\)
B. \(\overrightarrow u = ( – 2;7).\)
C. \(\overrightarrow u = ( – 3;5).\)
D. \(\overrightarrow u = (4; – 3).\)
4. : Trong mặt phẳng Oxy, cho \(A(2; – 3),{\rm{ }}B(0;1)\). Tìm tọa độ của vectơ \(\overrightarrow {AB} \).
A. \(\overrightarrow {AB} = \left( {4;2} \right)\).
B. \(\overrightarrow {AB} = \left( {2; – 4} \right)\).
C. \(\overrightarrow {AB} = \left( { – 2;4} \right)\).
D. \(\overrightarrow {AB} = \left( { – 2; – 4} \right)\).
5. : Trong mặt phẳng Oxy, cho \(A(1; – 1),{\rm{ }}B(2; – 3)\). Tìm tọa độ điểm \(D\) sao cho \(\overrightarrow {AD} = 3\overrightarrow {AB} .\)
A. \(D(4; – 7)\). B. \(D( – 4; – 1)\).
C. \(D(4; – 1)\). D. \(D( – 4;1).\)
6. : Cho hình bình hành ABCD. Khẳng định nào sau đây đúng?
A. \(\overrightarrow {AC} = \overrightarrow {BD} \).
B. \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \).
C. \(\overrightarrow {AB} = \overrightarrow {CD} \).
D. \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \).
7. : Trong mặt phẳng Oxy, cho \(A(4; – 3),{\rm{ }}B(2; – 1)\). Tìm tọa độ trung điểm \(I\) của đoạn thẳng \(AB\).
A. \(I\left( {2; – 2} \right)\). B. \(I\left( {6; – 4} \right)\).
C. \(I\left( { – 2;2} \right)\). D. \(I\left( {3; – 2} \right)\).
8. : Cho tập hợp \(A = \left\{ {1;2;4;5} \right\};\,\,B = \left\{ {2;4;6} \right\}\). Xác định tập hợp \(A \cup B\).
A. \(\left\{ {1;2;4;5;6} \right\}\).
B. \(\left\{ {1;5} \right\}\)
C. \(\left\{ {1;2;3;4;5;6} \right\}\).
D. \(\left\{ {2;4} \right\}\).
Advertisements (Quảng cáo)
9. : Tìm tập xác định của hàm số \(y = \sqrt {3x + 6} \).
A. \(\left( { – \infty ; – 2} \right]\).
B. \(\left[ { – 2; + \infty } \right)\).
C. \(\left[ {2; + \infty } \right)\).
D. \(\left( { – 2; + \infty } \right)\).
1.0 : Cho \(\left( P \right):y = – {x^2} + 2x + 3\). Chọn khẳng định đúng ?.
A. Hàm số đồng biến trên \(\left( { – \infty ;1} \right)\) và nghịch biến trên \(\left( {1; + \infty } \right)\).
B. Hàm số đồng biến trên \(\left( {1; + \infty } \right)\) và nghịch biến trên \(\left( { – \infty ;1} \right)\).
C. Hàm số đồng biến trên \(\left( { – 1; + \infty } \right)\) và nghịch biến trên \(\left( { – \infty ; – 1} \right)\).
D. Hàm số đồng biến trên \(\left( { – \infty ; – 1} \right)\)và nghịch biến trên\(\left( { – 1; + \infty } \right)\).
1.1 : Hàm số nào sau đây là hàm số chẵn ?
A. \(y = {x^4}\)
B. \(y = {x^4} + 1\).
C. \(y = {x^3}\).
D. \(y = {x^3} + 1.\)
1.2 : Cho tập hợp \(A = \left[ { – 2;5} \right);\,\,B = \left( {2;10} \right)\). Xác định tập hợp \(A \cap B\).
A. \(\left[ { – 2;2} \right)\). B. \(\left( {2;5} \right)\).
C. \(\left( {5;10} \right)\). D. \(\left[ { – 2;10} \right)\).
1.3 : Cho tập hợp \(A = \left\{ {x \in Z|\left( {x + 4} \right)\left( {{x^2} – 3x + 2} \right) = 0} \right\}\). Viết tập hợp \(A\) bằng cách liệt kê phần tử.
A. \(A = \left\{ {1;2;4} \right\}\).
B. \(A = \left\{ { – 1;2;3} \right\}\).
C. \(A = \left\{ {1;2; – 4} \right\}\).
D. \(A = \left\{ {1;2;3} \right\}\).
Advertisements (Quảng cáo)
1.4 : Tìm tập nghiệm của phương trình \(\sqrt {{x^2} – x – 2} = \sqrt {x – 2} \).
A. \(S = \left\{ { – 1;2} \right\}\).
B. \(S = \left\{ 0 \right\}.\)
C. \(S = \left\{ 2 \right\}\).
D. \(S = \left\{ {0;2} \right\}\).
1.5 : Tìm tập nghiệm của phương trình \(\sqrt {x – 5} = 2\).
A. \(S = \left\{ 3 \right\}\). B. \(S = \left\{ 9 \right\}\).
C. \(S = \emptyset \). D. \(S = \left\{ 7 \right\}\).
1.6 : Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, AC, BC. Hỏi \(\overrightarrow {BM} + \overrightarrow {MP} \) bằng vectơ nào?
A. \(\overrightarrow {MN} \) . B. \(\overrightarrow {BA} \).
C. \(\overrightarrow {BC} \). D. \(\overrightarrow {AP} \).
1.7 : Tìm trục đối xứng của parabol \(y = 2{x^2} + 4x – 1\).
A. \(x = 1\). B. \(x = 2\).
C. \(x = – 2\). D. \(x = – 1\) .
1.8 : Tìm nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + y – 3 = 0\\x – 3y + 1 = 0\end{array} \right.\).
A. \(( – 2; – 1)\) B. \((3;1)\).
C. \((2;3)\). D. \((2;1)\).
1.9 : Tìm a để đường thẳng \(y = ax – 1\) đi qua điểm \(M\left( {1;3} \right)\).
A. \(a = 2\). B. \(a = 4\).
C. \(a = 1\). D. \(a = 0\).
2.0 : Điểm nào dưới đây thuộc đồ thị hàm số \(y = 3x – 1\).
A. \((1;1)\). B. \((2;5)\).
C. \((2;3)\). D. \((0;1)\)
B. PHẦN TỰ LUẬN: (6đ)
Bài 1 . (2.0đ) Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {x^2} – 4x + 3\)
Bài 2 . (1.0đ) Giải phương trình \(\sqrt {x – 1} = x – 3\)
Bài 3 . (2.0đ) Trong mp Oxy, cho ba điểm \(A\left( {1;1} \right);\,\,B\left( {3;2} \right);\,\,C\left( {4; – 1} \right)\).
a) Tìm tọa độ điểm \(D\) sao cho \(ABCD\) là hình bình hành.
b) Tìm tọa độ điểm \(M\) thỏa mãn \(\overrightarrow {AM} = 2\overrightarrow {AB} – \overrightarrow {BC} \).
Bài 4 . (1.0đ) Xác định \(m\) để phương trình \({x^2} + 1 = mx\) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa \({x_1} – {x_2} = 1\) (giả sử \({x_1} > {x_2}\)).
A. PHẦN TRẮC NGHIỆM
|
1. C |
2. C |
3. D |
4. C |
5. A |
|
6. D |
7. D |
8. A |
9. B |
10. A |
|
11. A |
12. B |
13. C |
14. C |
15. B |
|
16. A |
17. D |
18. D |
19. B |
20. B |
B. PHẦN TỰ LUẬN: (6đ)
Bài 1: +) TXĐ: \(D = R\).
+) Tọa độ đỉnh \(I\left( {2; – 1} \right)\)
+) Trục đối xứng \(x = 2\)
+) Tính biến thiên:
Hàm số đồng biến trên \(\left( {2; + \infty } \right)\)
Hàm số nghịch biến trên \(\left( { – \infty ;2} \right)\).
+) Bảng biến thiên:
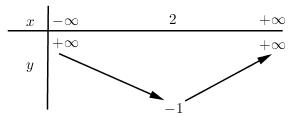+) Đồ thị:
Giao Ox: Cho \(y = 0 \Rightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\)
Giao Oy: Cho \(x = 0 \Rightarrow y = 3\)
Bài 2: \(\begin{array}{l}\sqrt {x – 1} = x – 3\\ \Leftrightarrow \left\{ \begin{array}{l}x – 3 \ge 0\\x – 1 = {\left( {x – 3} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\x – 1 = {x^2} – 6x + 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\{x^2} – 7x + 10 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left[ \begin{array}{l}x = 5\\x = 2\end{array} \right.\end{array} \right. \Leftrightarrow x = 5\end{array}\)
Vậy tập nghiệm của phương trình là \(S = \left\{ 5 \right\}\).
Bài 3: a) Để ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \)
\(\begin{array}{l} \Leftrightarrow \left( {2;1} \right) = \left( {4 – {x_D}; – 1 – {y_D}} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}2 = 4 – {x_D}\\1 = – 1 – {y_D}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 2\\{y_D} = – 2\end{array} \right.\\ \Rightarrow D\left( {2; – 2} \right)\end{array}\)
Vậy \(D\left( {2; – 2} \right)\).
b) Ta có \(\overrightarrow {AB} = \left( {2;1} \right);\,\,\overrightarrow {BC} = \left( {1; – 3} \right) \\\Rightarrow 2\overrightarrow {AB} – \overrightarrow {BC} = \left( {3;5} \right)\)
\(\begin{array}{l} \Rightarrow \overrightarrow {AM} = \left( {3;5} \right) \\\Rightarrow \left( {{x_M} – 1;{y_M} – 1} \right) = \left( {3;5} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}{x_M} – 1 = 3\\{y_M} – 1 = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_M} = 4\\{y_M} = 6\end{array} \right. \\ \Rightarrow M\left( {4;6} \right)\end{array}\).
Vậy \(M\left( {4;6} \right)\).
Bài 4: \({x^2} + 1 = mx \Leftrightarrow {x^2} – mx + 1 = 0\)
Để phương trình có hai nghiệm phân biệt \( \Leftrightarrow \Delta = {m^2} – 4 > 0 \Leftrightarrow \left[ \begin{array}{l}m > 2\\m < – 2\end{array} \right.\)
Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}{x_2} = 1\end{array} \right.\)
Ta có:
\(\begin{array}{l}{x_1} – {x_2} = 1 \\\Rightarrow {\left( {{x_1} – {x_2}} \right)^2} = 1\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} – 4{x_1}{x_2} = 1\\ \Leftrightarrow {m^2} – 4 = 1 \Leftrightarrow {m^2} = 5 \\\Leftrightarrow m = \pm \sqrt 5 \,\,\left( {tm} \right)\end{array}\)
Vậy \(m = \pm \sqrt 5 \).
