PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
1. : Tìm điều kiện của ẩn số x của phương trình \(\sqrt {x + 1} = 2 – x\) xác định:
A. \(x \le – 1\) B. \(x \le 2\)
C. \(x \ge – 1\) D. \(x \ge 2\)
2. : Điểm nào sau đây thuộc đồ thị hàm số \(y = 2x – 3\)?
A. \(N\left( {1;1} \right)\)
B. \(P\left( { – 2; – 7} \right)\)
C. \(M\left( {0;3} \right)\)
D. \(Q\left( { – 1;5} \right)\)
3. : Parabol \(y = {x^2} + 1\) nhận điểm nào sau đây làm đỉnh của nó?
A. \(O\left( {0;0} \right)\) B. \(I\left( {1;0} \right)\)
C. \(K\left( {0;1} \right)\) D. \(J\left( { – 1;0} \right)\)
4. : Cho tứ giác ABCD. Có tất cả bao nhiêu vectơ (khác vectơ \(\overrightarrow 0 \)) có điểm đầu và điểm cuối là các đỉnh của tứ giác đó?
A. 8 B. 12
C. 4 D. 16
5. : Trong hệ trục tọa độ Oxy, cho hai điểm \(M\left( { – 1;0} \right);\,\,N\left( {2; – 3} \right)\). Tìm tọa độ của vectơ \(\overrightarrow {NM} \).
A. \(\overrightarrow {NM} = \left( { – 3;3} \right)\)
B. \(\overrightarrow {NM} = \left( {3; – 3} \right)\)
C. \(\overrightarrow {NM} = \left( { – 2;0} \right)\)
D. \(\overrightarrow {NM} = \left( {1; – 3} \right)\)
6. : Cho các phát biểu sau:
(1) Hôm nay các em có khỏe không?
(2) Số 1320 là một số lẻ.
(3) 13 là một số nguyên tố.
(4) 2018 là một số chẵn
(5) Chúc các em kiểm tra đạt kết quả tốt.
(6) \({x^2} + 8x + 12 \ge 0\)
Trong các phát biểu trên có tất cả bao nhiêu phát biểu là mệnh đề ?
A. 4 B. 3
C. 5 D. 2
7. : Tìm tập xác định \(D\) của hàm số \(y = \dfrac{{{x^2} + 1}}{{x – 2}}\) ?
A. \(D = R\backslash \left\{ { – 2} \right\}\)
B. \(D = R\backslash \left\{ 2 \right\}\)
C. \(D = R\backslash \left\{ 0 \right\}\)
D. \(D = R\)
8. : Phương trình \({x^2} – 4x + 3 = 0\) có tập nghiệm là tập hợp nào sau đây ?
A. \(T = \left\{ { – 3; – 1} \right\}\)
B. \(W = \left\{ {1;3} \right\}\)
C. \(S = \left( {1;3} \right)\)
D. \(V = \left( { – 3; – 1} \right)\)
9. : Cho ba điểm A, B, C bất kì. Mệnh đề nào sau đây đúng ?
A. \(\overrightarrow {CA} + \overrightarrow {AB} = \overrightarrow {CB} \)
B. \(\overrightarrow {AC} – \overrightarrow {CB} = \overrightarrow {AB} \)
C. \(\overrightarrow {BA} + \overrightarrow {CA} = \overrightarrow {BC} \)
D. \(\overrightarrow {BC} – \overrightarrow {AC} = \overrightarrow {AB} \)
1.0 : Trong mặt phẳng tọa độ Oxy cho hai điểm \(A\left( { – 3;2} \right);\,\,B\left( {1;5} \right)\). Khoảng cách giữa hai điểm A và B bằng bao nhiêu?
A. 53 B. \(\sqrt {53} \)
C. \(25\) D. 5
1.1 : Trong mặt phẳng tọa độ Oxy cho các vectơ \(\overrightarrow a = \left( { – 2;1} \right);\,\,\overrightarrow b = \left( {1; – 3} \right);\,\,\overrightarrow c = \left( {0;2} \right)\). Tính tọa độ của vectơ \(\overrightarrow u = \overrightarrow a + \overrightarrow b + \overrightarrow c \).
Advertisements (Quảng cáo)
A. \(\overrightarrow u = \left( { – 1;6} \right)\)
B. \(\overrightarrow u = \left( {3;0} \right)\)
C. \(\overrightarrow u = \left( { – 1;0} \right)\)
D. \(\overrightarrow u = \left( {3;6} \right)\)
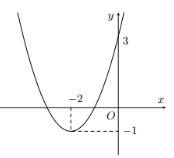
1.2 : Hàm số nào sau đây có đồ thị như hình vẽ bên?
A. \(y = – 2{x^2} – 8x + 3\)
B. \(y = 2{x^2} + 8x + 3\)
C. \(y = – {x^2} – 4x + 3\)
D. \(y = {x^2} + 4x + 3\)
1.3 : Cho hai tập hợp \(I = \left( { – 10;1} \right)\) và \(J = \left( { – 1;10} \right]\). Hãy xác định \(I \cup J\).
A. \(I \cup J = \left( { – 10;1} \right]\)
B. \(I \cup J = \left[ {1;10} \right]\)
C. \(I \cup J = \left( { – 1;1} \right)\)
D. \(I \cup J = \left( { – 10;10} \right]\)
1.4 : Liệt kê các phần tử của tập hợp \(H = \left\{ {x \in Z| – 2 \le x < 3} \right\}\).
A. \(H = \left\{ { – 2; – 1;0;1;2} \right\}\)
B. \(H = \left\{ { – 1;0;1;2} \right\}\)
C. \(H = \left\{ { – 2; – 1;0;1;2;3} \right\}\)
D. \(H = \left\{ {0;1;2;3} \right\}\)
1.5 : Cho hai tập hợp \(A = \left\{ { – 1;0;2;5} \right\}\) và \(B = \left\{ {1;2;3;5} \right\}\). Xác định tập hợp \(A\backslash B\).
A. \(A\backslash B = \left\{ { – 1;0} \right\}\)
B. \(A\backslash B = \left\{ {1;3} \right\}\)
C. \(A\backslash B = \left\{ { – 1;0;1;2;3;5} \right\}\)
D. \(A\backslash B = \left\{ {2;5} \right\}\)
1.6 : Cho các số thực a, b thỏa mãn điều kiện \(a – b – c = 6;\,\,b = a – 9;\,\,c = b + 7\). Tính giá trị của biểu thức \(P = 3a – 2b + c\).
A. \(P = 4\)
B. \(P = 10\)
C. \(P = – 48\)
D. \(P = 26\)
1.7 : Trong mặt phẳng Oxy cho tam giác ABC với \(A\left( {1;1} \right);\,\,B\left( { – 1;0} \right);\,\,C\left( { – 2;3} \right)\). Tọa độ trọng tâm G của tam giác ABC.
A. \(G\left( { – 2;4} \right)\)
Advertisements (Quảng cáo)
B. \(G\left( { – 2;2} \right)\)
C. \(G\left( { – \dfrac{2}{3};\dfrac{4}{3}} \right)\)
D. \(G\left( { – \dfrac{2}{3};0} \right)\)
1.8 : Xác định kết quả của \(\left( { – \infty ;1} \right] \cap \left[ { – 2;3} \right]\).
A. \(\left( { – \infty ;3} \right]\) B. \(\left( {1;3} \right]\)
C. \(\left( { – \infty ; – 2} \right)\) D. \(\left[ { – 2;1} \right]\)
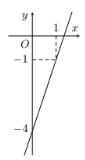
1.9 : Hàm số nào sau đây có đồ thị như hình bên ?
A. \(y = – 3x – 4\)
B. \(y = 2x – 3\)
C. \(y = 3x – 4\)
D. \(y = – 2x + 1\)
2.0 : Trong hệ tọa độ Oxy cho \(I\left( { – 3;2} \right);\,\,J\left( { – 1;3} \right);\,\,K\left( {4; – 3} \right)\). Tìm tọa độ điểm L để tứ giác IJKL là hình bình hành.
A. \(L\left( {2; – 4} \right)\)
B. \(L\left( {0;2} \right)\)
C. \(L\left( {6; – 2} \right)\)
D. \(L\left( { – 8;8} \right)\)
2.1 : Tìm tập xác định của hàm số \(y = 2\sqrt {x + 4} – 1\).
A. \(D = \left( { – 3; + \infty } \right)\)
B. \(D = \left[ { – 4; + \infty } \right)\)
C. \(D = \left[ { – 3; + \infty } \right)\)
D. \(D = \left( { – 4; + \infty } \right)\)
2.2 : Cho tam giác ABC có trọng tâm G và M là trung điểm của BC. Mệnh đề nào sau đây sai?
A. \(\overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \)
B. \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \)
C. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
D. \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = – 3\overrightarrow {MG} \)
2.3 : Mệnh đề nào sau đây sai?
A. \(\overrightarrow {OM} – \overrightarrow {ON} = \overrightarrow {NM} \)
B. \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \)
C. \(\overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \)
D. \(\overrightarrow {AC} – \overrightarrow {BD} = \overrightarrow {AD} – \overrightarrow {BC} \)
2.4 : Tìm tập nghiệm S của phương trình \(\dfrac{{x + 1}}{{x – 1}} – 1 = \dfrac{{3x}}{{x + 1}}\).
A. \(S = \left\{ { – 1;1} \right\}\)
B. \(S = \left\{ { – 1;\dfrac{2}{3}} \right\}\)
C. \(S = \left\{ { – \dfrac{1}{3};2} \right\}\)
D. \(S = \left\{ 0 \right\}\)
2.5 : Cho hình vuông ABCD cạnh bằng 2a. Tính độ dài của vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \)?
A. \(4a\) B. \(2a\)
C. \(2a\sqrt 2 \) D. \(a\sqrt 2 \)
2.6 : Phương trình nào sau đây là phương trình hệ quả của phương trình \(\dfrac{{{x^2} + x}}{{x + 1}} = 3\)?
A. \(3\left( {{x^2} + x} \right) = x + 1\)
B. \({x^2} – 2x – 3 = 0\)
C. \({x^2} + x = 3\)
D. \({x^2} + x = 0\)
2.7 : Cặp số \(\left( {x;y} \right)\) nào sau đây là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x – 3y = 7\\3x – y = 5\end{array} \right.\)?
A. \(\left( {10;1} \right)\) B. \(\left( {2;1} \right)\)
C. \(\left( { – 1; – 8} \right)\) D. \(\left( {1; – 2} \right)\)
2.8 : Tính tổng các nghiệm của phương trình \(\sqrt {{x^2} – 8x} = 3\).
A. 10 B. 8
C. -10 D. -9
2.9 : Hiện nay tuổi của cha gấp bốn lần tuổi của con và tổng số tuổi của hai cha con là 50. Hỏi bao nhiêu năm nữa tuổi cha gấp 3 lần tuổi con?
A. 5 năm B. 7 năm
C. 6 năm D. 8 năm
3.0 : Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với \(A\left( {3;4} \right);\,\,B\left( {4; – 1} \right)\) và \(C\left( {2; – 3} \right)\). Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác ABC.
A. \(I\left( {3;\dfrac{2}{3}} \right)\) B. \(I\left( {7;2} \right)\)
C. \(I\left( {9;2} \right)\) D. \(I\left( { – 1;1} \right)\)
3.1 : Trong mặt phẳng Oxy cho các điểm \(E\left( {3; – 2} \right);\,\,F\left( { – 1; – 3} \right)\). Tìm tọa độ điểm G thuộc trục hoành sao cho G thuộc đường thẳng EF.
A. \(G\left( { – \dfrac{{11}}{5};0} \right)\)
B. \(G\left( {11;0} \right)\)
C. \(G\left( {0; – \dfrac{{11}}{4}} \right)\)
D. \(G\left( {0; – \dfrac{{11}}{2}} \right)\)
3.2 : Cho hai tập hợp \(M = \left\{ {x \in R|x \le 4} \right\}\) và \(N = \left[ {m + 1;10} \right]\) với m là tham số. Tìm giá trị của m để \(M \cap N\) là một đoạn có độ dài bằng 10.
A. \(m = 5\) B. \(m > 3\)
C. \(m = – 7\) D. \(m \le 3\)
PHẦN II : TỰ LUẬN
1. : Giải phương trình \(3x – \sqrt {{x^2} + x + 4} = x – 2\)
2. : Trong mặt phẳng tọa độ Oxy cho các điểm \(A\left( {1;1} \right);\,\,B\left( { – 1;2} \right);\,\,C\left( { – 3; – 2} \right)\).
a) Tìm tọa độ điểm D để \(\overrightarrow {AD} = 2\overrightarrow {BC} \).
b) Tìm tọa độ điểm E thuộc trục tung sao cho \(CE = BC\).

I. PHẦN TRẮC NGHIỆM
|
1. C |
2. B |
3. C |
4. B |
5. A |
|
6. B |
7. B |
8. B |
9. A |
10. D |
|
11. C |
12. D |
13. D |
14. A |
15. A |
|
16. D |
17. C |
18. D |
19. C |
20. A |
|
21. B |
22. D |
23. D |
24. C |
25. C |
|
26. B |
27. D |
28. B |
29. A |
30. D |
|
31. B |
32. C |
|
|
|
II. PHẦN TỰ LUẬN
1. : \(\begin{array}{l}3x – \sqrt {{x^2} + x + 4} = x – 2\\ \Leftrightarrow 2x + 2 = \sqrt {{x^2} + x + 4} \\ \Leftrightarrow \left\{ \begin{array}{l}2x + 2 \ge 0\\{\left( {2x + 2} \right)^2} = {x^2} + x + 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge – 1\\4{x^2} + 8x + 4 = {x^2} + x + 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge – 1\\3{x^2} + 7x = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge – 1\\\left[ \begin{array}{l}x = 0\\x = – \dfrac{7}{3}\end{array} \right.\end{array} \right. \Leftrightarrow x = 0\end{array}\)
Vậy nghiệm của phương trình là \(x = 0\).
2. : a) Ta có : \(\overrightarrow {BC} = \left( { – 2; – 4} \right)\). Gọi \(D\left( {{x_D};{y_D}} \right) \Rightarrow \overrightarrow {AD} = \left( {{x_D} – 1;{y_D} – 1} \right)\).
\(\begin{array}{l}\overrightarrow {AD} = 2\overrightarrow {BC} \\ \Leftrightarrow \left\{ \begin{array}{l}{x_D} – 1 = – 4\\{y_D} – 1 = – 8\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_D} = – 3\\{y_D} = – 7\end{array} \right. \Rightarrow D\left( { – 3; – 7} \right)\end{array}\).
b) Gọi \(E\left( {0;{y_E}} \right) \in Oy\).
Ta có: \(CE = BC \Leftrightarrow C{E^2} = B{C^2} \) \(\Leftrightarrow {3^2} + {\left( {{y_E} + 2} \right)^2} = {2^2} + {4^2}\)
\(\begin{array}{l} \Leftrightarrow {\left( {{y_E} + 2} \right)^2} = 11\\ \Leftrightarrow \left[ \begin{array}{l}{y_E} = \sqrt {11} – 2\\{y_E} = – \sqrt {11} – 2\end{array} \right.\end{array}\)
Vậy \(E\left( {0;\sqrt {11} – 2} \right)\) hoặc \(E\left( {0; – \sqrt {11} – 2} \right)\).