
I. PHẦN TRẮC NGHIỆM ( 3đ) Học sinh điền đáp án đúng vào bảng sau:
1. . Cho tập hợp \(A = \left\{ {0;1;2;3;4} \right\}\). Chọn khẳng định sai.
A. \(\emptyset \subset A\)
B. \(\left\{ {1;2;4} \right\} \subset A\)
C. \(\left\{ { – 1;0;1} \right\} \subset A\)
D. \(0 \in A\)
2. . Cho mệnh đề P(x): “\(\forall x \in R,{x^2} + x + 1 > 0\)”. Mệnh đề phủ định của mệnh đề P(x) là:
A. “\(\exists x \in R,{x^2} + x + 1 \le 0\)”
B. “Không tồn tại \(x \in R,{x^2} + x + 1 > 0\)”
C. “\(\forall x \in R,{x^2} + x + 1 \le 0\)”
D. “\(\forall x \in R,{x^2} + x + 1 < 0\)”
3. . Cho tập hợp \(A = \left[ { – \dfrac{1}{2}; + \infty } \right)\). Khi đó tập hợp \({C_R}A\) là:
A. R
B. \(\left( { – \infty ; – \dfrac{1}{2}} \right]\)
C. \(\left( { – \infty ; – \dfrac{1}{2}} \right)\)
D. \(\emptyset \)
4. . Tập xác định của hàm số y = \(\dfrac{{x – 1}}{{{x^2} – x + 3}}\) là:
A. R
B. \(\left( { – \infty ;1} \right)\)
C. R\ {1 }
D. Æ
5. . Số nghiệm của phương trình \(\left( {{x^2} – 16} \right)\sqrt {3 – x} = 0\) là:
A. 1 nghiệm.
B. 3 nghiệm.
C. 0 nghiệm.
D. 2 nghiệm.
6. . Cho hàm số\(y = f(x) = 3{x^4} – {x^2} + 2\). Trong các mệnh đề sau, mệnh đề nào đúng?
A. \(y = f\left( x \right)\) là hàm số không chẵn và không lẻ
B. \(y = f\left( x \right)\)là hàm số chẵn trên R
C. \(y = f\left( x \right)\)là hàm số lẻ trên R
D. \(y = f\left( x \right)\) là hàm số vừa chẵn vừa lẻ trên R
7. . Hàm số\(y = \left| {2x + 10} \right|\) là hàm số nào sau đây:
A. \(y = \left\{ \begin{array}{l}2x + 10,…x \ge – 5\\2x – 10,…x < – 5\end{array} \right.\)
B. \(y = \left\{ \begin{array}{l}2x + 10,…x \ge – 5\\ – 2x + 10,…x < – 5\end{array} \right.\)
C. \(y = \left\{ \begin{array}{l}2x + 10,…x \ge 5\\ – 2x – 10,…x < 5\end{array} \right.\)
D. \(y = \left\{ \begin{array}{l}2x + 10,…x \ge – 5\\ – 2x – 10,…x < – 5\end{array} \right.\)
Advertisements (Quảng cáo)
8. . Cho hàm số \(y = – 3{x^2} – 4x + 3\) có đồ thị (P). Trục đối xứng của (P) là đường thẳng có phương trình:
A. \(x = \dfrac{4}{3}\)
B. \(x = – \dfrac{4}{3}\)
C. \(x = \dfrac{2}{3}\)
D. \(x = – \dfrac{2}{3}\)
9. . Cho hàm số\(y = {x^2} – 4x + 3\), khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng \(\left( { – \infty ;2} \right)\)và nghịch biến trên khoảng \(\left( {2; + \infty } \right)\)
B. Hàm số nghịch biến trên khoảng \(\left( { – \infty ; – 1} \right)\)và đồng biến trên khoảng \(\left( { – 1; + \infty } \right)\)
C. Hàm số nghịch biến trên khoảng \(\left( { – \infty ; – 2} \right)\)và đồng biến trên khoảng \(\left( { – 8; + \infty } \right)\)
D. Hàm số nghịch biến trên khoảng \(\left( { – \infty ;2} \right)\)và đồng biến trên khoảng \(\left( {2; + \infty } \right)\)
10 . Trong hệ trục \(\left( {O;\overrightarrow i ;\overrightarrow j } \right)\), tọa độ của vectơ \(\overrightarrow i + \overrightarrow j \) là:
A. (-1; 1) B. (0; 1).
C. (1; 0) D. (1; 1)
11 . Cho ABCD là hình bình hành có A(1;3), B(-2;0), C(2;-1). Toạ độ điểm D là:
A. (5;2) B. (4;-17)
C. (4;-1) D. (2;2)
12 . Trong mặt phẳng tọa độ Oxy, cho A(5; 2), B(10; 8). Tọa độ của vectơ \(\overrightarrow {AB} \) là:
A. (2; 4) B. (5; 6)
C. (5; 10) D. (-5; -6)
13 (NB). Trong mp Oxy, cho \(\overrightarrow a = (1; – 2)\), \(\overrightarrow b = (3;4)\), \(\overrightarrow c = (5; – 1)\). Toạ độ vectơ \(\overrightarrow u = 2.\overrightarrow a + \overrightarrow b – \overrightarrow c \) là:
A. \((0; – 1)\) B. \(( – 1;0)\)
C. \((1;0)\) D. \((0;1)\)
14 . Trong mp Oxy cho tam giác ABC có A(2;-3),B(4;1), trọng tâm G(-4;2). Khi đó tọa độ điểm C là:
A. \(\left( {\dfrac{2}{3};0} \right)\)
Advertisements (Quảng cáo)
B. (-18;8)
C. (-6;4)
D. (-10;10)
15 . Trong mặt phẳng tọa độ Oxy , cho A(1 ; 0), B(0 ; 3), C(-3; -5). Tọa độ của điểm M thuộc trục Ox sao cho \(\left| {2\overrightarrow {MA} – 3\overrightarrow {MB} + 2\overrightarrow {MC} } \right|\) nhỏ nhất là :
A. M( 4;5) B. M( 0; 4)
C. M( -4; 0) D. M( 2; 3)
II. PHẦN TỰ LUẬN ( 7đ)
Câu 1 . (2đ)
a) Lập bảng biến thiên và vẽ đồ thị hàm số \(y = – {x^2} – 2x + 3\)
b) Tìm m để phương trình: \({x^2} – 2mx + {m^2} – 2m + 1 = 0\) có hai nghiệm \({x_1};{x_2}\) sao cho biểu thức \(T = {x_1}{x_2} + 4\left( {{x_1} + {x_2}} \right)\) nhỏ nhất.
2. . ( 3đ) Giải các phương trình sau:
a) \(\left| {2x – 1} \right| = 3x – 4\)
b) \(\sqrt {2{x^2} – 4x + 9} = x + 1\)
c) \(\left( {x + 1} \right)\sqrt {{x^2} – 2x + 3} = {x^2} + 1{\rm{ }}\)
Câu 3 . (2đ)
a) Cho tứ giác ABCD. Chứng minh rằng: \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} – \overrightarrow {BC} \).
b) Cho DABC có trọng tâm G. Gọi M, N là các điểm xác định bởi \(\overrightarrow {AM} = 2\overrightarrow {AB} \), \(\overrightarrow {AN} = \dfrac{2}{5}\overrightarrow {AC} \). Chứng minh rằng: M, N, G thẳng hàng.

I. PHẦN TRẮC NGHIỆM
|
1. C |
2. A |
3. C |
4. A |
5. D |
|
6. B |
7. D |
8. D |
9. D |
10. D |
|
11. A |
12. B |
13. D |
14. B |
15. C |
II. PHẦN TỰ LUẬN
1. a) +Tập xác định \(D = R\).
+Bảng biến thiên:
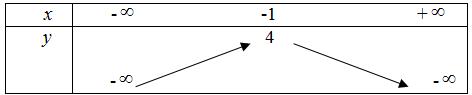
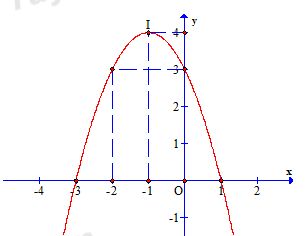
+ Vẽ đồ thị hàm số
+ Đỉnh \(I\left( { – 1;4} \right)\)
+ Trục đối xứng \(x = – 1\)
+ Giao với trục tung \(A\left( {0;3} \right)\)
+ Giao với trục hoành tại \(B\left( {1;0} \right);\,\,B’\left( { – 3;0} \right)\).
Để phương trình có nghiệm thì: \(\Delta ‘ \ge 0 \Leftrightarrow 2m – 1 \ge 0 \Leftrightarrow m \ge \dfrac{1}{2}\)
b) Ta có: \(\Delta ‘ = {m^2} – {m^2} + 2m – 1 = 2m – 1\).
Để phương trình có 2 nghiệm \( \Leftrightarrow 2m – 1 \ge 0 \Leftrightarrow m \ge \dfrac{1}{2}\).
Với \(m \ge \dfrac{1}{2}\) theo định lí Viét ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = {m^2} – 2m + 1\end{array} \right.\).
\(T = {x_1}{x_2} + 4\left( {{x_1} + {x_2}} \right) \) \(= {m^2} – 2m + 1 + 8m = {m^2} + 6m + 1\) suy ra \(T = f\left( m \right) = {m^2} + 6m + 1\).
BBT:
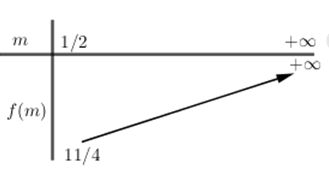
Dựa vào BBT của\(f\left( m \right)\) trên \(\left[ {\dfrac{1}{2}; + \infty } \right)\) ta tìm được GTNN của T bằng\(\dfrac{{11}}{4}\) khi\(m = \dfrac{1}{2}\).
Vậy \({T_{\min }} = \dfrac{{11}}{4} \Leftrightarrow m = \dfrac{1}{2}\).
2. a) Nếu \(x \ge \dfrac{1}{2}\): Phương trình (1) trở thành \(2x – 1 = 3x – 4 \Leftrightarrow x = 3\) (t/m\(x \ge \dfrac{1}{2}\)).
Vậy \(x = 3\) là một nghiệm của phương trình (1).
Nếu\(x < \dfrac{1}{2}\): Phương trình (1) trở thành \( – 2x + 1 = 3x – 4 \Leftrightarrow x = 1\)(không t/m \(x < \dfrac{1}{2}\)).
Vậy\(x = 1\) không là nghiệm của phương trình (1)
Kết luận: Tập nghiệm \(S = \left\{ 3 \right\}\)
b) \(\sqrt {2{x^2} – 4x + 9} = x + 1\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\2{x^2} – 4x + 9 = {\left( {x + 1} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge – 1\\{x^2} – 6x + 8 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 4\end{array} \right.\,\,\,\,\left( {tm} \right)\end{array}\)
Kết luận: Nghiệm của phương trình là\(x = 2\); \(x = 4\).
c) Đặt \(t = \sqrt {{x^2} – 2x + 3} \) \(\Rightarrow {t^2} = {x^2} – 2x + 3 \) \(\Rightarrow {x^2} = {t^2} + 2x – 3\)
Phương trình trở thành \(\left( {x + 1} \right)t = {t^2} + 2x – 2\)
\( \Leftrightarrow {t^2} – \left( {x + 1} \right)t + \left( {2x – 2} \right) = 0{\rm{ }}\left( 1 \right)\)
Ta xem \(\left( 1 \right)\) như là phương trình bậc hai với ẩn là t và x là tham số, lúc đó:
\(\Delta = {x^2} + 2x + 1 – 8x + 8 = {x^2} – 6x + 9 = {\left( {x – 3} \right)^2}\)
\( \Rightarrow \left[ \begin{array}{l}t = \dfrac{{x + 1 + x – 3}}{2} = x – 1\\t = \dfrac{{x + 1 – x + 3}}{2} = 2\end{array} \right.\).
Với \(t = \sqrt {{x^2} – 2x + 3} = x – 1 \) \(\Leftrightarrow {x^2} – 2x + 3 = {x^2} – 2x + 1{\rm{ }}\left( {VN} \right)\).
Với \(t = \sqrt {{x^2} – 2x + 3} = 2\) \( \Leftrightarrow {x^2} – 2x + 3 = 4 \) \(\Leftrightarrow {x^2} – 2x – 1 = 0 \Leftrightarrow x = 1 \pm \sqrt 2 \).
Vậy nghiệm của phương trình là \(x = 1 \pm \sqrt 2 \).
3. \(a)\,\,VT = \overrightarrow {AD} + \overrightarrow {DB} + \overrightarrow {CB} + \overrightarrow {BD}\) \( = \overrightarrow {AD} + \overrightarrow {CB} \) \(= \overrightarrow {AD} – \overrightarrow {BC} = VP\)
b) \(\overrightarrow {AM} = 2\overrightarrow {AB} \) \(\Leftrightarrow \overrightarrow {GM} – \overrightarrow {GA} = 2\overrightarrow {GB} – 2\overrightarrow {GA} \) \( \Leftrightarrow \overrightarrow {GM} = 2\overrightarrow {GB} – \overrightarrow {GA} \)
\(\overrightarrow {AN} = \dfrac{2}{5}\overrightarrow {AC} \) \( \Leftrightarrow \overrightarrow {GN} – \overrightarrow {GA} = \dfrac{2}{5}\overrightarrow {GC} – \dfrac{2}{5}\overrightarrow {GA} \) \( \Leftrightarrow \overrightarrow {GN} = \dfrac{2}{5}\overrightarrow {GC} + \dfrac{3}{5}\overrightarrow {GA} \)\( \Leftrightarrow 5\overrightarrow {GN} = 2\overrightarrow {GC} + 3\overrightarrow {GA} \)
\(\overrightarrow {GM} + 5\overrightarrow {GN} = \)\(2\overrightarrow {GB} – \overrightarrow {GA} \)+\(2\overrightarrow {GC} + 3\overrightarrow {GA} \) =\(2\overrightarrow {GA} + 2\overrightarrow {GB} \)+\(2\overrightarrow {GC} \)=\(\overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {GM} = – 5\overrightarrow {GN} \). Vậy G, M, N thẳng hàng.






