
PHẦN TRẮC NGHIỆM
1. : Biết rằng phương trình \(\sqrt {21x + 190} = x + 10\) có hai nghiệm phân biệt là a và b. Tính \(P = ab\left( {a + b} \right)\).
A. \(P = 60\) B. \(P = 90\)
C. \(P = – 60\) D. \(P = – 90\)
2. : Phương trình \({\left( {x + 1} \right)^2} = 3x + 9\) là phương trình hệ quả của phương trình nào sau đây?
A. \(\sqrt {x + 1} = 3x + 9\)
B. \(\sqrt {x + 1} = \sqrt {3x – 9} \)
C. \(x + 1 = \sqrt {3x + 9} \)
D. \(x + 1 = 3\left( {x + 3} \right)\)
3. : Cho một tam giác có độ dài ba cạnh lần lượt là 4cm, 7cm và 9cm. Góc lớn nhất của tam giác có cosin bằng bao nhiêu?
A. \( – \dfrac{{19}}{{21}}\) B. \(\dfrac{{\sqrt {19} }}{{21}}\)
C. \( – \dfrac{2}{7}\) D. \(\dfrac{2}{7}\)
4. : Biết rằng phương trình \({x^3} – 2{x^2} – 8x + 9 = 0\) có ba nghiệm phân biệt, trong dó có đúng một nghiệm âm có dạng \(\dfrac{{a – \sqrt b }}{c}\) (với a, b, c là các số tự nhiên và phân số \(\dfrac{a}{c}\) tối giản). Tính \(S = a + b + c\).
A. \(S = 40\) B. \(S = 38\)
C. \(S = 44\) D. \(S = 42\)
5. : Trong mặt phẳng tọa độ Oxy cho các điểm \(A\left( {1; – 17} \right);\,\,B\left( { – 11; – 25} \right)\). Tìm tọa độ điểm C thuộc BA sao cho \(BC = \sqrt {13} \).
A. \(C\left( { – 8; – 23} \right)\)
B. \(C\left( { – 2; – 19} \right)\)
C. \(C\left( { – 14; – 27} \right)\)
D. \(\left( { – 9; – 22} \right)\)
6. : Tam giác ABC có \(AB = 4a;\,\,AC = 9a\) và trung tuyến \(AM = \dfrac{{\sqrt {158} a}}{2}\). Tính theo a độ dài của cạnh BC.
A. \(BC = \dfrac{{\sqrt {230} }}{2}a\)
B. \(BC = 6a\)
C. \(BC = 9a\)
D. \(BC = a\sqrt {18} \)
7. : Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình \(2{x^2} – 6x – 3 = 0\). Đặt \(M = \left( {2{x_1} – 1} \right)\left( {2{x_2} – 1} \right)\). Khẳng định nào sau đây là khẳng định đúng?
A. \(M = – 9\) B. \(M = – 12\)
C. \(M = – 11\) D. \(M = – 8\)
8. : Trong mặt phẳng tọa độ Oxy cho các vectơ \(\overrightarrow u = \left( {3; – 2} \right)\) và \(\overrightarrow v = \left( {{m^2};4} \right)\) với m là số thực. Tìm m để hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) cùng phương.
A. \(m = – 6\)
B. \(m = \pm \sqrt 6 \)
C. \(m = \sqrt 6 \)
D. \(m \in \emptyset \)
9. : Tìm tập xác định D của phương trình \(\dfrac{{x – 2}}{{{x^2} – 4}} = \sqrt {x – 1} \).
A. \(D = \left[ {1; + \infty } \right)\)
B. \(D = \left[ { – 2;2} \right]\)
C. \(D = \left[ {1; + \infty } \right)\backslash \left\{ 2 \right\}\)
Advertisements (Quảng cáo)
D. \(D = R\backslash \left\{ { \pm 2} \right\}\)
1.0 : Tập nghiệm S của phương trình \(3{x^4} – 2{x^2} – 1 = 0\)
A. \(S = \left\{ 1 \right\}\)
B. \(S = \left\{ {1; – \dfrac{1}{3}} \right\}\)
C. \(S = \left\{ { – 1;1} \right\}\)
D. \(S = \left\{ { \pm 1; \pm \dfrac{1}{{\sqrt 3 }}} \right\}\)
1.1 : Trong mặt phẳng tọa độ Oxy cho điểm \(A\left( {3; – 7} \right)\) và điểm B. Biết rằng điểm \(M\left( { – 1;2} \right)\) là trung điểm của đoạn thẳng AB. Điểm B không thuộc đường thẳng nào sau đây?
A. \({d_1}:\,\,y = 2x + 11\)
B. \({d_2}:\,\,y = x + 16\)
C. \({d_3}:\,\,y = – 2x + 1\)
D. \({d_4}:\,\,y = – x + 6\)
1.2 : Cho hình vuông ABCD có \(AB = 2\). Tích vô hướng \(\overrightarrow {AB} .\overrightarrow {CA} \) có giá trị bằng bao nhiêu ?
A. \( – 4\) B. \( – 2\)
C. \(2\) D. 4
1.3 : Tìm tất cả các giá trị của tham số m để đồ thị \(\left( P \right)\) của hàm số \(y = {x^2} + 2x + m – 2\) cắt trục hoành tại hai điểm phân biệt?
A. \(m < 1\) B. \(m > 3\)
C. \(m > 1\) D. \(m < 3\)
1.4 : Tìm giá trị của m để đỉnh I của đồ thị hàm số \(y = {x^2} – 4x + m\) thuộc đường thẳng \(y = 2017\).
A. \(m = 2019\) B. \(m = 2015\)
C. \(m = 2013\) D. \(m = 2021\)
1.5 : Biết rằng parabol \(\left( P \right):\,\,y = a{x^2} + bx + c\) đi qua hai điểm \(A\left( {1;2} \right)\) và \(B\left( {2;6} \right)\). Tính giá trị của biểu thức \(Q = 3a + b\).
A. \(Q = – 4\)
B. \(Q = 4\)
C. \(Q = 0\)
Advertisements (Quảng cáo)
D. Không đủ dữ kiện để tính.
1.6 : Cho phương trình \(\left( {x + 2} \right)\left( {x – 5} \right) + 3\sqrt {x\left( {x – 3} \right)} = 0\). Khi đặt \(t = \sqrt {x\left( {x – 3} \right)} \) thì phương trình đã cho trở thanh phương trình nào sau đây?
A. \({t^2} + 3t – 10 = 0\)
B. \({t^2} + 3t + 10 = 0\)
C. \({t^2} – 3t – 10 = 0\)
D. \({t^2} – 3t + 10 = 0\)
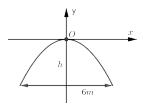
1.7 : Một chiếc cổng hình parabol có phương trình \(y = – \dfrac{1}{2}{x^2}\). Biết cổng có chiều cao \(d = 6\) mét (như hình bên). Hãy tính chiều cao h của cổng?
A. \(h = 5m\) B. \(h = 3m\)
C. \(h = 4,5m\) D. \(h = 3,5m\)
1.8 : Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình \(\left| {x – 5} \right| = \left| {3x – 7} \right|\). Tính \(T = \left| {{x_1} – {x_2}} \right|\).
A. \(T = 3\) B. \(T = 2\)
C. \(T = 4\) D. \(T = 1\)
1.9 : Biết rằng hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 5\\mx – 4y = 2\end{array} \right.\) vô nghiệm khi tham số mnhận giá trị bằng \({m_0}\). Khẳng định nào sau đây là khẳng định đúng?
A. \({m_0} \in \left( {\dfrac{1}{2};\dfrac{3}{2}} \right)\)
B. \({m_0} \in \left( { – \dfrac{5}{2}; – \dfrac{3}{2}} \right)\)
C. \({m_0} \in \left( { – \dfrac{3}{2}; – \dfrac{1}{2}} \right)\)
D. \({m_0} \in \left( {\dfrac{3}{2};\dfrac{5}{2}} \right)\)
2.0 : Cho tam giác ABC có diện tích bằng 12. Nếu tăng độ dài cạnh AB lên gấp 3 lần, đồng thời giảng độ dài cạnh AC còn một nửa và giữ nguyên độ lớn của góc A thì được một tam giác có diện tích S bằng bao nhiêu?
A. \(S = 18\) B. \(S = 16\)
C. \(S = 8\) D. \(S = 60\)
PHẦN TỰ LUẬN
1. (1,0đ) : Giải các phương trình:
\(a)\,\,\left| {x – 1} \right| = \left| {{x^2} + 2x} \right|\)
\(b)\,\,\sqrt {2\left( {x + 1} \right)} – 2 = \sqrt {x – 1} \)
2. (1,0đ) : Cho phương trình \(\left( {x – 2} \right)\left( {2{x^2} – 2x + 3m – 1} \right) = 0\,\,\left( 1 \right)\) với m là tham số thực.
a) Tìm m để phương trình (1) nhận \({x_0} = 3\) là một nghiệm.
b) Tìm m để phương trình (1) có 3 nghiệm phân biệt trong đó có đúng 1 nghiệm âm.
3. (1,0đ) : Trong mặt phẳng tọa độ Oxy cho tam giác ABC có \(A\left( {2;2} \right);\,\,B\left( {5;3} \right)\) và \(C\left( {4; – 4} \right)\). Chứng minh rằng tam giác ABC vuông và tìm tọa độ điểm D sao cho bốn điểm A, B, C, D lập thành một hình chữ nhật.
4. (1,0đ) : Cho tam giác ABC có \(AC = 7cm,\,\,BC = 10cm\) và \(\widehat {BAC} = {60^0}\). Tính \(\sin \widehat {ABC}\) và tính độ dài cạnh AB (yêu cầu tính ra kết quả chính xác, không tính xấp xỉ).

PHẦN TRẮC NGHIỆM
|
1. D |
2. C |
3. C |
4. A |
5. A |
|
6. C |
7. C |
8. D |
9. C |
10. C |
|
11. A |
12. A |
13. D |
14. D |
15. B |
|
16. A |
17. C |
18. B |
19. B |
20. A |
PHẦN TỰ LUẬN
1. \(\begin{array}{l}a)\,\,\left| {x – 1} \right| = \left| {{x^2} + 2x} \right|\\ \Leftrightarrow \left[ \begin{array}{l}x – 1 = {x^2} + 2x\\x – 1 = – {x^2} – 2x\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} + x + 1 = 0\,\,\left( \text{vô nghiệm} \right)\\{x^2} + 3x – 1 = 0\end{array} \right.\\ \Leftrightarrow x = \dfrac{{ – 3 \pm \sqrt {13} }}{2}\end{array}\)
Vậy tập nghiệm của phương trình là \(S = \left\{ {\dfrac{{ – 3 \pm \sqrt {13} }}{2}} \right\}\).
\(\begin{array}{l}b)\,\,\sqrt {2\left( {x + 1} \right)} – 2 = \sqrt {x – 1} \\ \Leftrightarrow \sqrt {2\left( {x + 1} \right)} = 2 + \sqrt {x – 1} \\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\2\left( {x + 1} \right) = 4 + x – 1 + 4\sqrt {x – 1} \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\x – 1 = 4\sqrt {x – 1} \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\{x^2} – 2x + 1 = 16x – 16\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\{x^2} – 18x + 17 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 17\end{array} \right.\,\,\left( {tm} \right)\end{array}\)
Vậy tập nghiệm của phương trình là \(S = \left\{ {1;17} \right\}\).
2. a) Thay \(x = 3\) vào phương trình ta có:
\(\left( {3 – 2} \right)\left( {{{2.3}^2} – 2.3 + 3m – 1} \right) = 0 \)
\(\Leftrightarrow 3m + 11 = 0 \Leftrightarrow m = – \dfrac{{11}}{3}\)
b) \(\left( {x – 2} \right)\left( {2{x^2} – 2x + 3m – 1} \right) = 0 \)
\(\Leftrightarrow \left[ \begin{array}{l}x = 2\\2{x^2} – 2x + 3m – 1 = 0\,\,\,\left( 2 \right)\end{array} \right.\)
Để phương trình (1) có 3 nghiệm phân biệt trong đó có đúng 1 nghiệm âm.
\( \Leftrightarrow \) Phương trình (2) có 2 nghiệm phân biệt trái dấu và khác 2.
\( \Leftrightarrow \left\{ \begin{array}{l}ac = 2\left( {3m – 1} \right) < 0\\{2.2^2} – 2.2 + 3m – 1 \ne 0\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}m < \dfrac{1}{3}\\m \ne – 1\end{array} \right.\)
\(\Rightarrow m \in \left( { – \infty ;\dfrac{1}{3}} \right)\backslash \left\{ { – 1} \right\}\).
Vậy để phương trình (1) có 3 nghiệm phân biệt trong đó có đúng 1 nghiệm âm thì \(m \in \left( { – \infty ;\dfrac{1}{3}} \right)\backslash \left\{ { – 1} \right\}\).
3.
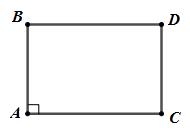
Ta có \(\overrightarrow {AB} = \left( {3;1} \right);\,\,\overrightarrow {AC} = \left( {2; – 6} \right);\)\(\,\,\overrightarrow {BC} = \left( { – 1; – 7} \right)\)
\( \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 3.2 + 1.\left( { – 6} \right) = 0\)
\(\Rightarrow AB \bot AC \Rightarrow \Delta ABC\) vuông tại A.
Để ABDC là hình bình hành
\(\begin{array}{l} \Leftrightarrow \overrightarrow {AB} = \overrightarrow {CD} \\ \Leftrightarrow \left( {3;1} \right) = \left( {{x_D} – 4;{y_D} + 4} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}{x_D} – 4 = 3\\{y_D} + 4 = 1\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}{x_D} = 7\\{y_D} = – 3\end{array} \right. \Rightarrow D\left( {7; – 3} \right)\end{array}\)
Hơn nữa \(\widehat {BAC} = {90^0}\,\,\left( {cmt} \right)\) nên ABDC là hình chữ nhật.
Vậy \(D\left( {7; – 3} \right)\).
4. Áp dụng định lí sin ta có:
\(\begin{array}{l}\dfrac{{AC}}{{\sin \widehat {ABC}}} = \dfrac{{BC}}{{\sin \widehat {BAC}}}\\ \Leftrightarrow \dfrac{7}{{\sin \widehat {ABC}}} = \dfrac{{10}}{{\sin {{60}^0}}}\\ \Leftrightarrow \sin \widehat {ABC} = \dfrac{{7.\sin {{60}^0}}}{{10}} = \dfrac{{7\sqrt 3 }}{{20}}\end{array}\)
Áp dụng định lí cosin ta có:
\(\begin{array}{l}\,\,\,\,\,\,\cos \widehat {BAC} = \dfrac{{A{B^2} + A{C^2} – B{C^2}}}{{2AB.AC}}\\ \Leftrightarrow \cos {60^0} = \dfrac{{A{B^2} + {7^2} – {{10}^2}}}{{2.AB.7}}\\ \Leftrightarrow 7AB = A{B^2} – 51\\ \Leftrightarrow A{B^2} – 7AB – 51 = 0\\ \Leftrightarrow \left[ \begin{array}{l}AB = \dfrac{{7 + \sqrt {253} }}{2}\\AB = \dfrac{{7 – \sqrt {253} }}{2} < 0\,\,\left( {ktm} \right)\end{array} \right.\\ \Rightarrow AB = \dfrac{{7 + \sqrt {253} }}{2}\end{array}\)






