
1. Cho m, n là hai số tự nhiên. Chứng minh rằng tích mn chia hết cho 7 khi và chỉ khi có ít nhất một trong hai số m, n chia hết cho 7.
2. Phát biểu mệnh đề đảo của định lí: “Trong một tam giác cân, các đường trung tuyến ứng với các cạnh bên bằng nhau”. Mệnh đề đảo đó đúng hay sai? Tại sao?
3. Cho hai tập hợp \(A = \left\{ {1;2;3;4;5;6} \right\}\) và \(B = \left\{ {2;4;6;8;10} \right\}\) . Tìm tất cả các tập hợp X sao cho \(X \subset A\) và \(X \subset B\) .Bài toán có bao nhiêu nghiệm?
4. Cho hai tập hợp .
a. Viết các tập hợp P, Q dưới dạng khoảng ( đoạn, nửa khoảng) hoặc hợp của các khoảng (đoạn, nửa khoảng).
b. Chứng minh rằng \({C_R}\left( {P \cup Q} \right) = {C_R}P \cap {C_R}Q\).
5. Cho hình chữ nhật có chiều dài \(5,86m \pm 0,05m\) và chiều rộng \(3,73m \pm 0,02m\)
a. Tính diện tích hình chữ nhật
b. Xác định các chữ số chắc của diện tích hình chữ nhật. Viết kết quả dưới dạng chuẩn.

1. Thuận: Cho tích mn chia hết cho 7. Chứng minh m hoặc n chia hết cho 7.
Giả sử có hai số tự nhiên m, n sao cho mn chia hết cho 7 và m, n đêu khong chia hết cho 7.
Đặt \(m= 7a + r\) và \(n= 7b + s\), với và \(r,s \in \left\{ { – 3; – 2; – 1;1;2;3} \right\}\) .
Khi đó \(mn = \left( {7a + r} \right)\left( {7b + s} \right) = 7\left( {7ab + as + br} \right) + rs\) .
Mà \(r,s \in \left\{ { – 3; – 2; – 1;1;2;3} \right\}\) nên \(rs \in \left\{ { – 9; – 6; – 4; – 3; – 2; – 1;1;2;3;4;6;9} \right\}\) .
Suy ra rs không chia hết cho 7. Do đó mn không chia hết cho 7. Trái với giả thiết.
Vậy nếu mn chia hết cho 7 thì m hoặc n không chia hết cho 7.
Đảo: Cho m hoặc n chia hết cho 7. Chứng minh tích mn chia hết cho 7.
Nếu m chia hết cho 7 thì \(m= 7a\), với . Suy ra \(mn= 7an\) chia hết cho 7.
Nếu n chia hết cho 7 thì \(n= 7b\), với . Suy ra \(mn= 7bm\) chia hết cho 7.
2. Mệnh đề đảo: “Nếu một tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân”.
Advertisements (Quảng cáo)
Mệnh đề này đúng.
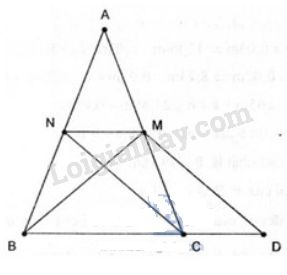
Chứng minh: Cho tam giác ABC có hai trung tuyến BM và CN bằng nhau.
Trên tia đối của tia CB lấy điểm D sao cho CD= NM.
Khi đó CDMN là hình bình hành. Suy ra NC= MD và NC // MD.
Mà BM= CN nên MB = MD.
Suya ra MBD là tam giác cân tại M.
Do đó \(\widehat {MBD}= \widehat {NCB}\) (đồng vị) nên \(\widehat {MBC} = \widehat {NCB}\).
Từ đó \(\Delta MBC = \Delta NCB\) .
Suy ra MC = NB hay AB = AC.
Vậy tam giác ABC cân tại A.
3. Do \(X \subset A\) và \(X \subset B\) nên \(X \subset A \cap B\) .
Mà \(A \cap B = \left\{ {2;4;6} \right\}\) .
Advertisements (Quảng cáo)
Do đó X là các tập sau: \(\emptyset ,\left\{ 2 \right\},\left\{ 4 \right\},\left\{ 6 \right\},\left\{ {2;4} \right\},\left\{ {2;6} \right\},\left\{ {4;6} \right\},\)\(\,\left\{ {2;4;6} \right\}\) .
Bài toán có 8 nghiệm.
4. a.Ta có
+) \(\left| {x – 2} \right| \le 3 \Leftrightarrow – 3 \le x – 2 \le 3\)
\(\Leftrightarrow – 1 \le x \le 5.\)
Suy ra \(P = \left[ { – 1;5} \right]\) .
+ \(\eqalign{ & \left| {x + 2} \right| > 4\cr& \Leftrightarrow \left[ \matrix{ x + 2 < – 4 \hfill \cr x + 2 > 4 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ x < – 6 \hfill \cr x > 2 \hfill \cr} \right..{\rm{ }} \cr & {\rm{Suy\; ra\; Q = }}\left( { – \infty ; – 6} \right) \cup \left( {2; + \infty } \right) \cr} \) .
b.Ta có
\(\eqalign{ & +)\; P \cup Q = \left( { – \infty ; – 6} \right) \cup \left[ { – 1; + \infty } \right).{\rm{ }} \cr & {\rm{Suy\; ra\; }}{{\rm{C}}_R}\left( {P \cup Q} \right) = \left[ { – 6; – 1} \right) \cr} \)
\(\eqalign{ & +)\; {C_R}P = \left( { – \infty ; – 1} \right) \cup \left( {5; + \infty } \right),\cr&\;\;{C_R}Q = \left[ { – 6;2} \right]. \cr & {\rm{Suy \;ra \;}}{{\rm{C}}_R}P \cap {C_R}Q = \left[ { – 6; – 1} \right) \cr} \) .
Vậy \({C_R}\left( {P \cup Q} \right) = {C_R}P \cap {C_R}Q\)
5. a. Ta có
+ \(a = 5,86m \pm 0,05m \)
\(\Rightarrow 5,86m – 0,05m \le a \le 5,85m + 0,05m\) .
+ \(b = 3,73m \pm 0,02m\)
\(\Rightarrow 3,73m – 0,02m \le b \le 3,73m + 0,02m\) .
Suy ra: \(21,8205{m^2} – 0,3045{m^2} \le ab \le 21,8205{m^2} \pm 0,3045{m^2}\) .
Vậy diện tích hình chữ nhật là \(S = 21,8205{m^2} \pm 0,3045{m^2}\) .
b. Sai số tuyệt đối của S là \({\Delta _S} = 0,3045{m^2}\) .
Xét chữ số hàng đơn vị của S.
Một nửa đơn vị của hàng này là \(\dfrac{1 }{2} \times 1{m^2} = 0,5{m^2} > {\Delta _S}\) .
Suy ra chữ số hàng phần chục là chữ số chắc.
Xét chữ số hàng chục của S.
Một nửa đơn vị của hàng này là \(\dfrac{1 }{2} \times 0,1{m^2} = 0,05{m^2} < {\Delta _S}\) .
Suy ra chữ số hàng phần chục là chữ số không chắc.
Vậy các chữ số chắc của S là các chữ số hàng đơn vị và hàng chục.
Dạng chuẩn của S là 21m2.






