
Chọn phương án đúng
1. Cho mệnh đề . Phủ định mệnh đề trên là
A.\(\forall x \in \mathbb{R},{x^2} < 0\)
B.\(\forall x \in \mathbb{R},{x^2} \le 0\)
C.\(\exists x \in \mathbb{R},{x^2} \le 0\)
D.\(\exists x \in \mathbb{R},{x^2} < 0\)
2. Cho mệnh đề chứa biến \(P(x):x + 15 \le {x^2} < 0,x \in \mathbb{R}.\) Mệnh đề nào sau đây là mệnh đề đúng
A.P(0)
B.P(5)
C.P(2)
D.P(4)
3. Trong các mệnh đề sau, mệnh đề nào không phải là định lý
A.\(\forall n \in \mathbb{N},{n^2} \;\vdots\; 2 \Rightarrow n \;\vdots \;2\)
B.\(\forall n \in \mathbb{N},{n^2} \;\vdots \;3 \Rightarrow n \;\vdots \;3\)
C.\(\forall n \in \mathbb{N},{n^2}\; \vdots \;9 \Rightarrow n \;\vdots \;9\)
D.\(\forall n \in \mathbb{N},{n^2}\; \vdots\; 6 \Rightarrow n \;\vdots\; 6\)
4. Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng
A.\(\forall x \in \mathbb{R},x > 1 \Rightarrow {x^2} > 1\)
B.\(\forall x \in \mathbb{R},x > – 1 \Rightarrow {x^2} > 1\)
C.\(\forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > 1\)
D.\(\forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > – 1\)
Advertisements (Quảng cáo)
5. Cho tập A có 5 phần tử. Số tập con có 2 phần tử của A là
A.8 B.10
C.12 D.14
6. Cho hai tập \(A = \left\{ {x \in \mathbb{R}|x + 3 < 5 + 2x} \right\},\)\(\;{\rm{ B = }}\left\{ {x \in \mathbb{R}|5x – 4 < 4X – 1} \right\}\)
Tất cả các số tự nhiên thuộc tập \(A \cap B\) là
A. \(0,1,2\) B. \(0,1\)
C. \(1,2\) D. \(-1,0,1,2\)
7. Cho số a<0. Điều kiện cần và đủ để hai tập \(( – \infty ;5a)\) và \(\left( {\dfrac{5}{a}; + \infty } \right)\) có giao khác rỗng là
A.\( – 1 \le a < 0\) B.\(a \le – 1\)
C.\(a < -1\) D.\(-1< a <0\)
8. Cho các tập hợp \(A = \left\{ {x \in \mathbb{R}|f(x) = 0} \right\},\)\(\;B = \left\{ {x \in \mathbb{R}|g(x) = 0} \right\}\) và
\(C = \left\{ {x \in \mathbb{R}|{f^2}(x) + {g^2}(x) = 0} \right\}\). Khi đó
A. \(C = A \cup B\) B. \(C = A\backslash B\)
C. \(C=B\backslash A\) D. \(A \cap B\)
Advertisements (Quảng cáo)
9. Cho các tập \(A = \left[ { – 5;4} \right],\)\(\,{\rm{ B = }}\left( { – 3;2} \right)\). Khi đó
A.\(A\backslash B = \left[ { – 5; – 4} \right] \cup \left[ {3;4} \right]\)
B.\(A\backslash B = \left[ { – 5;3} \right] \cup \left[ {2;4} \right]\)
C.\(A\backslash B = \left[ { – 5; – 3} \right]\)
D.\(A\backslash B = \left[ { – 5;\left. { – 3} \right) \cup \left( {2;\left. 4 \right]} \right.} \right.\)
1.0. Mệnh đề nào sau đây là mệnh đề đúng
A.\(E \subset E \cap F\)
B.\(E \cup F \subset F\)
C.\(E = (E\backslash F) \cup (E \cap F)\)
D.\(E \cup F = (E\backslash F) \cup (F\backslash E)\)

1. Chọn C. Phủ định của mệnh đề “\(\forall x \in X,P(x)\)” là mệnh đề “\(\exists x \in X,\overline {P(x)} \) “.
2.Chọn B. \(P(5):5 + 15 \le 25\) là mệnh đề đúng.
3. Chọn C. Với n = 3 thì n2 = 9 chia hết cho 9 nhưng n không chia hết cho 9.
4. Chọn A. Hiển nhiên x > 1 thì x2 > 1.
5. Chọn B. Cho \(A = \left\{ {a;b;c;d;e} \right\}\) . Các tập con có hai phần tử của A là
\(\left\{ {a;b} \right\},\left\{ {a;c} \right\},\left\{ {a;d} \right\},\left\{ {a;e} \right\},\left\{ {b;c} \right\},\)\(\;\left\{ {b;d} \right\},\left\{ {b;e} \right\},\left\{ {c;d} \right\},\left\{ {c;e} \right\},\left\{ {d;e} \right\}\) .
Có tất cả 10 tập như vậy.
6. Chọn A. Ta có: \(x + 3 < 5 + 2x \Leftrightarrow x > – 2\) . Suy ra \(A = \left( { – 2; + \infty } \right)\) .
Tương tự \(5x – 4 < 4x – 1 \Leftrightarrow x < 3\) . Suy ra \(B = \left( { – \infty ;3} \right)\) .
7. Chọn D. Hai tập đã cho có giao khác rỗng khi và chỉ khi
\(\dfrac{5}{a} < 5a \Rightarrow {a^2} < 1 \Rightarrow – 1 < a < 0\) (do \( a < 1\)) .
8. Chọn D
\(\begin{array}{l}x \in C \Leftrightarrow {f^2}(x) + {g^2}(x) = 0\\ \Leftrightarrow \left\{ \begin{array}{l}f(x) = 0\\g(x) = 0\end{array} \right.\\{\rm{ }} \Leftrightarrow \left\{ \begin{array}{l}x \in A\\x \in B\end{array} \right. \Leftrightarrow x \in A \cap B\end{array}\) .
Vậy \(C = A \cap B\) .
9. Chọn B. Biểu diễn các tập hợp trên trục số để suy ra kết quả.
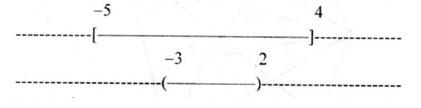
1.0. Chọn C.
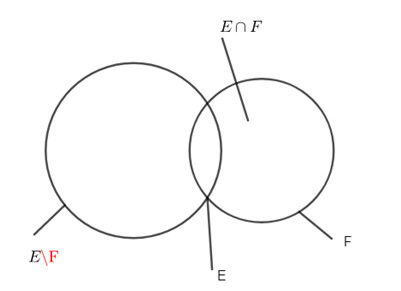
Kiểm tra hệ thức \(E = \left( {E\backslash F} \right) \cup \left( {E \cap F} \right)\) bằng biểu đồ Ven.

