Giải bài 36,37,38 ,39,40,41 ,42,43 trang 82,83 SGK Toán 9 tập 2: Góc có đỉnh ở bên trong-bên ngoài đường tròn

Chi tiết Lời giải bài tập bài 36,37,38 trang 82; Bài 39,40,41 ,42,43 trang 83 Toán 9 tập 2: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn.

Bài 36. Cho đườngtròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh rằng tam giác AEH là tam giác cân.

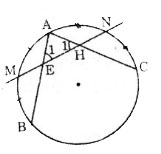
∠E1 và ∠H1 là các góc có đỉnh ở trong (O) nên:

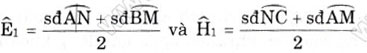
Mà cung AN = cung NC và Cung BM = cung AM (giả thiết)
⇒ ∠E1 = ∠H1. Vậy tam giác ∆AEN cân tại A (đpcm).

---

Bài 37. Cho đườngtròn (O) và hai dây AB, AC bằng nhau. Trên cung nhỏ AC lấy một điểm M. Gọi S là giao điểm của AM và BC. Chứng minh ∠ASC = ∠MCA.

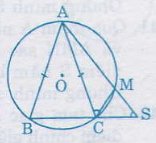
Ta có: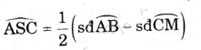

(∠ASC là góc có đỉnh nằm bên ngoài đườngtròn (O))

và ∠MCA= 1/2sđAM  (2)(góc nội tiếp chắn cung AM)

Theo giả thiết thì:     AB = AC => cung AB = cung AC (3)

Từ (1), (2), (3) suy ra:

---

Bài 38. Trên một đườngtròn, lấy liên tiếp ba cung AC, CD, DB sao cho sđcung AC =sđCD = sđ DB = 60⁰. Hai đường thẳng AC và BD cắt nhau tại E. Hai tiếp tuyến của đườngtròn tại B và C cắt nhau tại T. Chứng minh rằng:

a) ∠AEB = ∠BTC;

b) CD là phân giác của ∠BCT

Giải.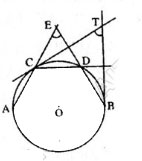

Ta có ∠AEB là góc có đỉnh ở bênngoài đườngtròn nên:

và ∠BTC cũng là góc có đỉnh ở bênngoài đườngtròn (hai cạnh đều là tiếp tuyến của đường-tròn) nên:

Vậy ∠AEB = ∠BTC
b) ∠DCT là góc tạo bởi tiếp tuyến và dây cung nên:

∠DCB là góc nội tiếp nênVậy ∠DCT = ∠DCB hay CD là tia phân giác của ∠BCT.

---

Bài 39. Cho AB và CD là hai đường kính vuông góc của đườngtròn (O). Trên cung nhỏ BD lấy một điểm M. Tiếp tuyến tại M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S.Chứng minh ES = EM.

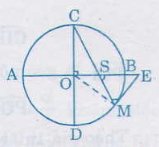
Ta có  ∠MSE = sđ (CA + BM)/2 (1)

( vì ∠MSE là góc có đỉnh S ở trong đường-tròn (O)).

∠CME =sđCM/2=  sđ(CB + BM)  (2)

( ∠CME là góc tạo bởi tiếp tuyến và dây cung).

Theo giả thiết cung CA = CB        (3)

Từ (1), (2), (3) ta có: ∠MSE = ∠CME từ đó ∆ESM là tam giác cân và ES = EM

---

Bài 40. Qua điểm S nằm bên ngoài đường-tròn (O), vẽ tiếp tuyến SA và cát tuyến SBC của đường-tròn. Tia phân giác của góc BAC cắt dây BC tại D. Chứng minh SA = SD.

---

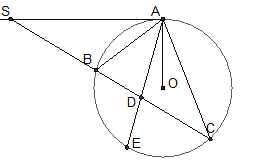
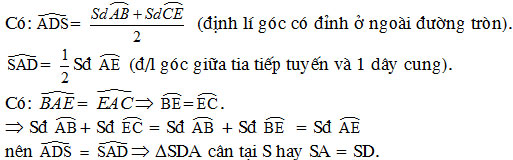
Bài 41 trang 83 . Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên trong đường-tròn. Chứng minh:  ∠A + ∠BSM =2∠CMN.

hướng dẫn bài 41:

---

Bài 42 trang 83 Toán 9 tập 2. Cho tam giác ABC nội tiếp đường tròn. P, Q, R theo thứ tự là các điểm chính giữa các cung bị chắn BC, CA, AB bởi các góc A, B, C.

a) Chứng minh AP ⊥ QR

b) AP cắt CR tại I. Chứng minh tam giác CPI là tam giác cân.

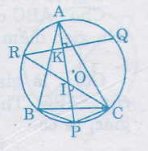
a) Gọi giao điểm của AP và QR là K.  ∠AKR là góc có đỉnh ở bêntrong đường-tròn nên ∠AKR = sđcung(AR +QC + CP)/2  =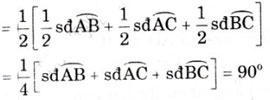

Vậy ∠AKR = 90⁰ hay AP ⊥ QR

b) ∠CIP  là góc cóđỉnh ở bêntrong đgtròn nên:

∠CIP = sđcung(AR +CP)/2     (1)

∠PCI góc nội tiếp, nên ∠PCI= (sđ cung RB + BP)/2       (2)

Theo giả thiết thì cung AR = RB  (3)

Cung CP = BP        (4)

Từ (1), (2), (3), (4) suy ra: ∠CIP = ∠PCI. Do đó ∆CPI cân.

---

Bài 43. Cho đgtròn (O) và hai dây cung song song AB, CD (A và C nằm trong cùng một nửa mặt phẳng bờ BD); AD cắt BC tại I

Chứng minh  ∠AOC =  ∠AIC.

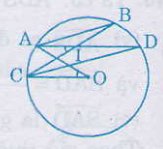
Theo giả thiết: Cung AC = cung BD (vì AB // CD)    (1)

∠AIC = sđ cung(AC +BD)/2(2)

Theo (1) suy ra:

∠AIC = sđ cung AC (3)

∠AOC = sđcung AC  (góc ở tâm chắn cung AC) (4)

So sánh (3), (4), ta có  ∠AOC =  ∠AIC.