[Có đáp án] Đề thi kì 1 lớp 10 môn Toán trường THPT Nguyễn Trung Trực 2015 theo chương trình chuẩn và nâng cao. Đề thi có 2 phân chung, riêng (Các em tùy chọn làm theo chương trình mình học)
Trường THPT Nguyễn Trung Trực
ĐỀ THI HỌC KỲ I NĂM HỌC 2015-2016
MÔN : TOÁN – LỚP 10
Thời gian làm bài : 90 phút
A.PHẦN CHUNG CHO TẤT CẢ THÍ SINH ( 7 điểm )
Bài 1: (1,0 điểm) Nêu mệnh đề phủ định của mệnh đề sau,xét xem mệnh đề phủ định đó đúng hay sai :
a) Phương trình x2 – 4x + 3 = 0 có nghiệm.
b) 22011 chia hết cho 8
c ) Có vô số số nguyên tố chia hết cho 3 .
d) x2 + x + 1 ≤ 0
Bài 2: (2,0 điểm)
Advertisements (Quảng cáo)
a) Cho A= {n ∈ N* / n < 6} và B={0;1;4;5;7}. Xác định A ∩ B và B\A
b) Tìm tập xác định của hàm số 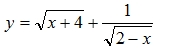
Bài 3: (2,0 điểm) Cho hàm số y = ax2 + bx + 3
a) Xác định a, b của hàm số biết đồ thị hàm số đi qua A(1;0) và B(-2;15)
b) Lập bảng biến thiên và vẽ đồ thị hàm số vừa tìm được ở câu a).
Bài 4: (2,0 điểm)
a) Cho ba điểm A(3;2), B(4;1), và C(1;5). Tìm toạ độ trọng tâm G của tam giác ABC và tìm tọa độ của điểm M để ABCM là hình bình hành.
b) Cho sinα =4/5, (00<α< 900). Tính giá trị của biểu thức
Advertisements (Quảng cáo)
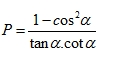
B.PHẦN RIÊNG ( 3 điểm )
Bài 5 ( Dành cho thí sinh học chương trình nâng cao )
a/ (1,0 điểm) Giải phương trình :![]()
b/ (1,0 điểm) Giải hệ phương trình![]()
c/ (1,0 điểm) Chứng minh rằng nếu a, b, c là độ dài các cạnh của một tam giác thì ta luôn có
![]()
Bài 6 ( Dành cho thí sinh học chương trình cơ bản )
a/ (1,0 điểm) Giải phương trình:![]()
b/ (1,0 điểm) Giải hệ phương trình :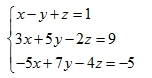
c/ (1,0 điểm) Chứng minh rằng nếu a, b, c là độ dài các cạnh của một tam giác thì ta luôn có: a2 + b2 + c2 < 2(ab + bc + ca)
————————- Hết ————————–
Đáp án và hướng dẫn chấm De thi hoc ki 1 lop 10 môn Toán trường THPT Nguyễn Trung Trực
 Dap an cau 1 va 2 De thi hoc ki 1 Toan lop 12
Dap an cau 1 va 2 De thi hoc ki 1 Toan lop 12
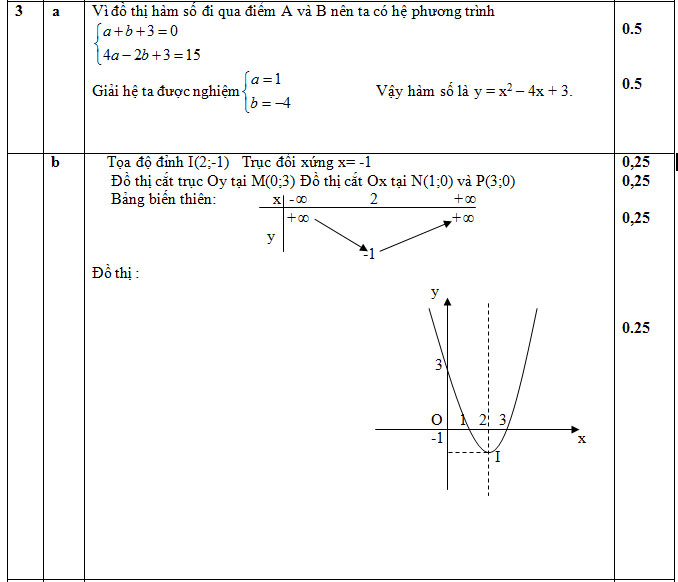 Dap an cau 3 De thi hoc ki 1 Toan lop 12
Dap an cau 3 De thi hoc ki 1 Toan lop 12
 Dap an cau 4 De thi hoc ki 1 Toan lop 12
Dap an cau 4 De thi hoc ki 1 Toan lop 12
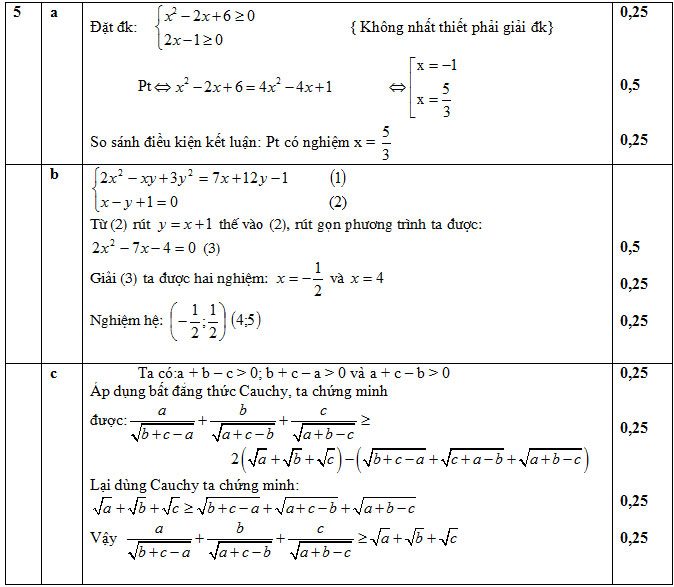 Dap an cau 5 De thi hoc ki 1 Toan lop 12 (Phan nang Cao)
Dap an cau 5 De thi hoc ki 1 Toan lop 12 (Phan nang Cao)
 Dap an cau 6 De thi hoc ki 1 Toan lop 12 (Phan co ban)
Dap an cau 6 De thi hoc ki 1 Toan lop 12 (Phan co ban)






