Đáp án và Giải bài 1, 2, 3, 4, 5, 6, 7 trang 68 SGK Đại số 10: Phương trình và hệ phương trình bậc nhất nhiều ẩn.
Bài 1. Cho hệPT
Tại sao không cần giải ta cũng kết luận được HPT này vô nghiệm ?
Ta thấy rằng nhân vế trái PT thứ nhất (7x -5y) với 2 thì được vế trái của PT2 (14x -10y). Trong khi đó nhân vế phải PT thứ nhất với 2 thì kết quả khác với vế phải PT2. Vậy chắc HPT vô nghiệm.
Gọn hơn, ta có: 
nên hệPT đã cho vô nghiệm.
Bài 2 trang 68. Giải các hệ phươngtrình
a) Giải bằng phương pháp thế: 2x – 3y = 1 ⇒ y = (2x -1)/3
Thế vào PT2:
Kết luận: HệPT có nghiệm duy nhất (11/7; 5/7).
Giải bằng phương pháp cộng đại số: Nhân hai vế của PT2 với -2 rồi cộng với Phươngtrinh1 ta được
b) Giải tương tự câu a).
Đáp số: (9/11; 7/11).
c) Để tránh tính toán trên các phân số ta nhân PT thứ nhất với 6, nhân PT2 với 12 ⇔
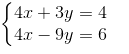
lấy PT1 trừ đi PT2 ta được:
d) Nhân mỗi PT với 10 ta được
Nhân PT1 với 2 cộng vào PT2 ta được
Advertisements (Quảng cáo)
Bài 3. Hai bạn Vân và Lan đến cửa hàng mua trái cây. Bạn Vân mua 10 quả quýt, 7 quả cam với giá tiền là 17 800 đồng. Bạn Lan mua 12 quả quýt, 6 quả cam hết 18 000 đồng. Hỏi giá tiền mỗi quả quýt và mỗi quả cam là bao nhiêu ?
Gọi x (đồng) là giá tiền một quả quýt và y (đồng) là giá tiền một quả cam. Điều kiện
x > 0, y > 0 ta có HPT:
Trả lời: Giá tiền một quả quýt: 800 đồng, một quả cam 1400 đông.
Bài 4. Có hai dây chuyền may áo sơ mi. Ngày thứ nhất cả hai dây chuyền may được 930 áo. Ngày thứ hai do dây chuyền thứ nhất tăng năng suất 18%, dây chuyền thứ hai tăng năng suất 15% nên cả hai dây chuyền may được 1083 áo. Hỏi trong ngày thứ nhất mỗi dây chuyền may được bao nhiêu áo sơ mi ?
Gọi số áo may được của dây chuyền thứ nhất và thứ hai ngày thứ nhất theo thứ tự là x, y (cái) thì ngày thứ hai các dây chuyền ấy may được 1,18x (cái) và 1,15y (cái). Điều kiện x, y nguyên dương. Ta có HPT:
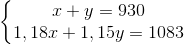⇔ x = 450; y = 480.
Kết luận: Ngày thứ nhất hai dây chuyền may được số áo tương ứng là 450 cái và 480 cái.
Bài 5. Giải các hệ phương trình
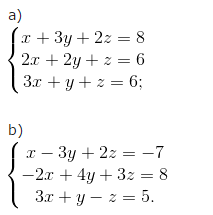
Đáp án bài 5: a) x + 3y + 2z = 8 ⇒ x = 8 – 3y – 2z.
Thế vào PT2 và thứ ba thì được
Giải hệ hai Pt với ẩn y và z:
Advertisements (Quảng cáo)
Nghiệm của Hệpt ban đầu là (1; 1; 2).
Ghi chú: Ta cũng có thể giảibằng phương pháp cộng đại số như sau: Nhân Pt1 với -2 rồi cộng vào pt2.
Nhân pt1 với -3 cộng vào PT3 thì được
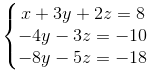
Giải HPT sau:
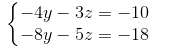
ta được kết quả như trên.
b)
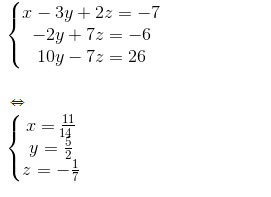
Bài 6 trang 68. Một cửa hàng bán áo sơ mi, quần âu nam và váy nữ. Ngày thứ nhất bán được 12 áo, 21 quần và 18 váy, doanh thu là 5 349 000 đồng. Ngày thứ hai bán được 16 áo, 24 quần và 12 váy, doanh thu là 5 600 000 đồng. Ngày thứ ba bán được 24 áo, 15 quần và 12 váy, doanh thu là 5 259 000 đồng. Hỏi giá bán mỗi áo, mỗi quần và mỗi váy là bao nhiêu ?
Đặt x, y, z theo thứ tự là giá tiền bán một áo sơ mi, một quần âu và một váy nữ. Điều kiện x, y, z >0. Ta có hệ pt:
(nghìn đồng) ⇔
Vậy giá tiền một áo là 98 nghìn, một quần âu nam là 125 nghìn và váy nữ là 86 nghìn.
Bài 7. Giải các HPT sau bằng máy tính bỏ túi (làm tròn kết quả đến chữ số thập phân thứ hai)
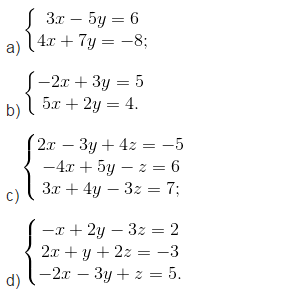
a) Nếu sử dụng máy tính CASIO fx-500 MS ta ấn liên tiếp các phím
thấy hiện ra màn hình x = 0.048780487.
Ấn tiếp phím 
ta thấy màn hình hiện ra y = -1.170731707.
Làm tròn kết quả đến chữ số thập phân thứ hai ta được nghiệm gần đúng của hệ phương trình là
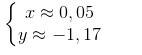
b) Ấn 
Kết quả x = 0.105263157. Ấn tiếp kết quả y = -1.736842105.
c) Ấn 
thấy hiện ra trên màn hình x=0.217821782.
Ấn tiếp phím ta thấy màn hình hiện ra y = 1.297029703.
Ấn tiếp phím trên màn hình hiện ra z = -0.386138613.
Vậy nghiệm gần đúng của HPT là (làm tròn kết quả đế chữ số thaaph phân thứ hai)
d) Thực hiện tương tự câu c).
Kết quả: x = -1.870967742;
y = -0.35483709;
z = 0.193548387.
![[THPT Nguyễn Thượng Hiền] tổ chức thi Toán khối 10 kì 2: Tìm tiêu cự, tọa độ các đỉnh, độ dài các trục của elip](https://dethikiemtra.com/wp-content/uploads/2018/04/THPT-Nguyễn-Thượng-Hiền-100x75.png)
