
Cho hình bình hành ABCD. Phân giác của \(\widehat A\) và \(\widehat C\) cắt đường chéo BD tại E và F. Chứng minh rằng hai đa giác ABCFE và ADCFE có diện tích bằng nhau

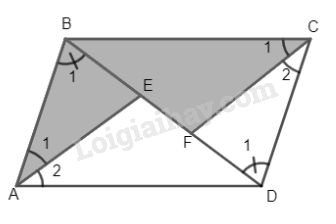
Theo giả thiết ABCD là hình bình hành \( \Rightarrow \widehat A = \widehat C\) .
Do AE và CF là hai phân giác của \(\widehat A\) và \(\widehat C\) nên:
Advertisements (Quảng cáo)
\(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {{C_1}} = \widehat {{C_2}}\)
Xét hai tam giác ABE và CDF có:
\(\widehat {{A_1}} = \widehat {{C_2}};AB = AD;\widehat {{B_1}} = \widehat {{D_1}}\) (so le trong)
\( \Rightarrow \Delta ADE = \Delta CBF\) (g.c.g)
Advertisements (Quảng cáo)
Tương tự \(\Delta ADE = \Delta CBF\)
\( \Rightarrow \left. \matrix{{S_{ABD}} = {S_{CDF}} \hfill \cr{S_{CBF}} = {S_{ADE}} \hfill \cr} \right\} \)\(\,\Rightarrow {S_{ABE}} + {S_{CBF}} = {S_{CDF}} + {S_{ADE}} \)
\(\Rightarrow {S_{ABCFE}} = {S_{ADCFE}}.\)






