Đề kiểm tra 45 phút Chương 1 – Mệnh đề, Tập hợp môn Đại số 10: Phát biểu và xét tính đúng sai của các mệnh đề P(5) và Q(6)

1. Cho hai mệnh đề chứa biến

P(n) : “3n² + 5 chia hết cho 5”, với \(n \in N\) .

Q(n): “ n chia hết cho 5”, với \(n \in N\) .

a. Phát biểu và xét tính đúng sai của các mệnh đề P(5) và Q(6).

b. Phát biểu và chứng minh định lí “\(\forall n \in N,P\left( n \right) \Rightarrow Q\left( n \right)\) “.

c. Phát biểu mệnh đề đảo của định lí trên. Mệnh đề này đúng hay sai? Nếu đúng hãy phát biểu gộp cả định lí thuận và định lí đảo.

2. Phát biểu mệnh đề đảo của định lí : “ Trong một hình thang cân, hai đường chéo bằng nhau”. Mệnh đề này đúng hay sai?  Tại sao?

3. Cho các tập hợp

a. Dùng kí hiệu đoạn, khoảng, nửa khoảng hay hợp của các đoạn, khoảng, nửa khoảng để viết lại các tập hợp trên.

b. Tìm \(A \cap B,A \cup B,C,A\left( {B\backslash C} \right)\) .

C. Cho \(D = \left( {a – 1;a + 1} \right]\) .Tìm điều kiện của a sao cho \(A \cap D \ne \emptyset \) .

4. Cho hình chữ nhật có chiều dài là \(15,86m \pm 0,03m\) và chiều rộng là \(8,73m \pm 0,02m\) .

a.Tính chu vi hình chữ nhật.

b.Xác định các chữ số chắc của chu vi hình chữ nhật. Viết kết quả dưới dạng chuẩn.

1. a.P(5): “80 chia hết cho 5” là mệnh đề đúng.

   Q(6): “6chia hết cho 5” là mệnh đề sai.

b. Phát biểu: “ Với mọi số tự nhiên n, nếu 3n² + 5 chia hết cho 5 thì n chia hết cho 5”

Chứng minh: Bằng phương pháp phản chứng.

Giả sử có số tự nhiên n sao cho 3n² + 5 chia hết cho 5 và n không chia hết cho 5.

Đặt n= 5k + r, với  và \(r \in \left\{ { \pm 1; \pm 2} \right\}\) .

Khi đó \(3{n^2} + 5 = 3{\left( {5k + r} \right)^2} + 5 \)\(\,= 5\left( {15{k^2} + 16k + 1} \right) + 3{r^2}\) .

Mà \(3{r^2} \in \left\{ {3;12} \right\}\) nên \(3{r^2}\)  không chia hết cho 5.

Suy ra \(3{n^2} + 5\)  không chia hết cho 5. Trái với giả thiết.

Vậy với mọi số tự nhiên n, nếu \(3{n^2} + 5\)  chia hết cho 5 thì n chia hết cho 5.

c. Mệnh đề đảo: “Với mọi số tự nhiên n, nếu n chia hết cho 5 thì \(3{n^2} + 5\)  chia hết cho 5” là mệnh đề đúng.

Định lí thuận đảo: “Điều kiện cần và đủ để số tự nhiên n chia hết cho 5 là số \(3{n^2} + 5\)  chia hết cho 5”.

2. Mệnh đề đảo: “Trong một hình thang nếu hai đường chéo bằng nhau thì hình thang đó cân”. Mệnh đề đảo này đúng.

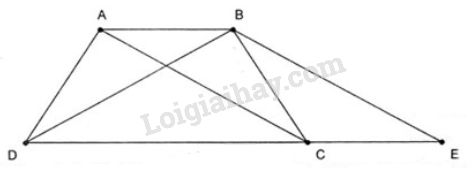
Chứng minh: Cho hình thang ABCD với hai đáy là AB và CD có hai đường chéo AC và BD bằng nhau.

Trên tia đối của tia CD lấy điểm E sao cho CE= AB.

Ta có ABEC là hình bình hành.

Suy ra BE = AC và BE // AC. Mà AC= BD nên BD= BE.

Do đó BDE là tam giác cân tại B.

Suy ra \(\widehat {BDE} = \widehat {BED}\).

Mặt khác \(\widehat {ACD} = \widehat {BED}\) (đồng vị) nên \(\widehat {ACD} = \widehat {BDC}\)

Từ đó \(\Delta ADC = \Delta BCD\) .

Vì vậy \(\widehat {ADC} = \widehat {BCD}\) hay ABCD là hình thang cân.

3. a. Ta có

+ \(\eqalign{  & \left| {x + {1 \over 2}} \right| \le {9 \over 2}\cr& \Leftrightarrow  – {9 \over 2} \le x + {1 \over 2} \le {9 \over 2}\cr& \Leftrightarrow  – 5 \le x \le 4.{\rm{ }}  \cr  & {\rm{Suy \;ra \;A = }}\left[ { – 5;4} \right] \cr} \) .

+ \(\eqalign{  & \left| {x + 1} \right| > 2 \Leftrightarrow \left[ \matrix{  x – 1 <  – 2 \hfill \cr  x – 1 > 2 \hfill \cr}  \right. \cr&\Leftrightarrow \left[ \matrix{  x <  – 1 \hfill \cr  x > 3 \hfill \cr}  \right..  \cr  & {\rm{ Suy\; ra\; B = }}\left( { – \infty ; – 1} \right) \cup \left( {3, + \infty } \right) \cr} \) .

+ \(\eqalign{  & \left| {x – 2} \right| < 4 \Leftrightarrow  – 4 < x – 2 < 4\cr& \Leftrightarrow  – 2 < x < 6.  \cr  & {\rm{ Suy\; ra\; C = }}\left( { – 2;6} \right) \cr} \) .

b. Ta có

\(A \cap B = \left[ { – 5; – 1} \right) \cup \left( {3;4} \right]\)

\({C_R}A = \left( { – \infty ; – 5} \right) \cup \left( {4; + \infty } \right),\)

\({\rm{ B\backslash C = }}\left( { – \infty ; – 2} \right] \cup \left[ {6; + \infty } \right)\)

Suy ra \({C_R}A \cap \left( {B\backslash C} \right) = \left( { – \infty ; – 5} \right) \cup \left[ {6, + \infty } \right)\) .

c. Ta có \(A \cap D \ne \emptyset \)

\(\Leftrightarrow \left\{ \matrix{  a – 1 < 4 \hfill \cr  a + 1 \ge  – 5 \hfill \cr}  \right.\)

\(\Leftrightarrow  – 6 \le a < 5\) .

4. 1) Ta có

+) \(a = 15,86m \pm 0,03m \)

\(\Rightarrow 15,86m – 0,03m \le a \le 15,86m + 0,03m.\)

+) \(b = 8,73m \pm 0,02m\)

\(\Rightarrow 8,73m – 0,02m \le b \le 8,73m + 0,02m.\)

Suy ra \(24,59m – 0,05m \le a + b \le 24,59m + 0,05m.\)

Do đó \(49,18m – 0,1m \le 2\left( {a + b} \right) \le 49,18 + 0,1m\) .

Vậy chu vi hình chữ nhật là \(P = 49,18m \pm 0,1m\) .

2) Sai số tuyệt của P là \({\Delta _P} = 0,1m\)

Xét chữ số hàng đơn vị của P. Một nửa đơn vị của hàng này là

\(\dfrac{1 }{ 2}m = 0,5m > {\Delta _P}\) . Suy ra chữ số hàng đơn vị là chữ số chắc.

Xét chữ số hàng phân chục của P. Một nửa đơn của hàng này là

\(\dfrac{1 }{ 2} \times 0,1 = 0,05 < {\Delta _P}\) . Suy ra chữ số hàng chục là chữ số không chắc.

Vậy P có các chữ số hàng đơn vị và hàng chục là các chữ số chắc.

Suy ra dạng chuẩn của P là 49m.