Cho hai góc kề bù \(\widehat {AOB}\) và \(\widehat {BOC}.\). Biết \(\widehat {AOB} = {60^o}.\) Tính \(\widehat {BOC}.\) … trong Kiểm tra Toán lớp 6 15 phút Chương 2 – Góc. Xem Đề và đáp án đầy đủ phía dưới đây
1. (4đ) Cho hai góc kề bù \(\widehat {AOB}\) và \(\widehat {BOC}.\)
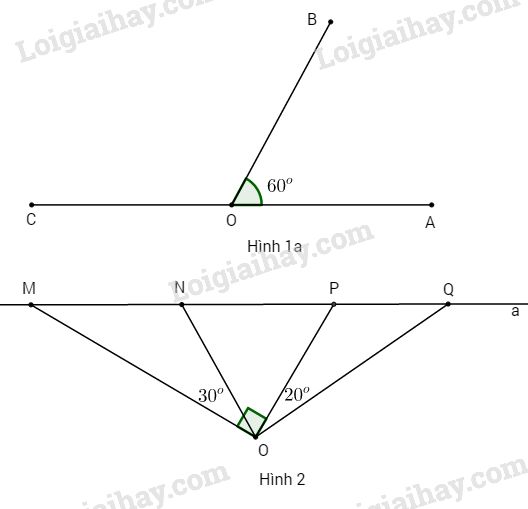
a) Biết \(\widehat {AOB} = {60^o}.\) Tính \(\widehat {BOC}.\)
b) Biết \(\widehat {AOB} – \widehat {BOC} = {36^o}.\) Tính \(\widehat {AOB}\) và \(\widehat {BOC}.\)
2. (6đ) Trên đường thẳng a lấy điểm M, N, P, Q theo thứ tự đó. Gọi O là điểm nằm ngoài đường thẳng a. Biết \(\widehat {MON} = {30^o},\)\(\widehat {POQ} = {20^o},\) \(\widehat {MOP} = {90^o}.\) Tính \(\widehat {NOP},\widehat {NOQ},\widehat {MOQ}.\)
|
Câu |
Đáp án |
Điểm |
|
1. (4đ) |
a) Vì hai góc \(\widehat {AOB}\) và \(\widehat {BOC}\) kề bù nên \(\widehat {AOB} + \widehat {BOC} = {180^o}.\) Biết \(\widehat {AOB} = {60^o}.\)Tính được \(\widehat {BOC} = {120^o}.\) b) Vì hai góc \(\widehat {AOB}\) và \(\widehat {BOC}\) kề bù nên \(\widehat {AOB} + \widehat {BOC} = {180^o}.\) Biết \(\widehat {AOB} – \widehat {BOC} = {36^o}\) Tính được: \(\widehat {AOB} = {108^o};\,\widehat {BOC} = {72^o}\) |
2đ 2đ |
|
2. (6đ) |
Chỉ rõ ON nằm giữa hai tia OM, OP nên có: \(\widehat {MON} + \widehat {NOP} = \widehat {MOP}\) Từ đó tính được: \(\widehat {NOP} = {60^o}\) Chỉ rõ tia OP nằm giữa hai tia ON, OQ nên có: \(\widehat {POQ} + \widehat {NOP} = \widehat {NOQ}\) Từ đó tính được: \(\widehat {NOQ} = {80^o}\) Chỉ rõ tia OP nằm giữa hai tia OM, OQ nên có: \(\widehat {POQ} + \widehat {MOP} = \widehat {MOQ}\) Từa đó tính được: \(\widehat {MOQ} = {110^o}\) |
2đ 2đ 2đ |
