Kiểm tra 15 phút Toán Chương 1 Hình học 8: Chứng minh tứ giác OEFC là hình thang và tứ giác OEIC là hình bình hành

Cho hình chữ nhật ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Lấy E nằm giữa hai điểm O và B. Gọi F là điểm đối xứng với điểm A qua E và I là trung điểm của CF. Chứng minh tứ giác OEFC là hình thang và tứ giác OEIC là hình bình hành … trong Kiểm tra 15 phút Toán Chương 1 Hình học 8. Xem Đề và đáp án đầy đủ phía dưới đây

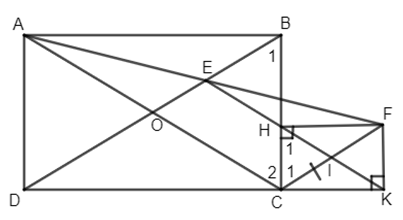
Cho hình chữ nhật ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Lấy E nằm giữa hai điểm O và B. Gọi F là điểm đối xứng với điểm A qua E và I là trung điểm của CF.

a) Chứng minh tứ giác OEFC là hình thang và tứ giác OEIC là hình bình hành.

b) Gọi H và K lần lượt là hình chiếu của điểm F trên các đường thẳng BC và CD. Chứng minh tứ giác CHFK là hình chữ nhật và I là trung điểm của đoạn HK.

c) Chứng minh ba điểm E, H, K thẳng hàng.

---

a) Ta có EA = EF (tính chất đối xứng)

 OA = OC (tính chất hai đường chéo của hình chữ nhật)

\( \Rightarrow OE\) là đường trung bình của \(\Delta ACF \Rightarrow OE//CF.\)

b) Ta có \(FH \bot BC\) hay \(\widehat {FHC} = {90^ \circ },\widehat {HCK} = {90^ \circ },\)\(\;\widehat {FKC} = {90^ \circ }(gt)\)

Do đó CHFK là hình chữ nhật (có ba góc vuông), I là trung điểm của đường chéo CF (gt) \( \Rightarrow I\) là trung điểm của đường chéo HK.

c) Ta có \(\Delta HIC\) cân (tính chất đường chéo hình chữ nhât) \( \Rightarrow \widehat C_1= \widehat H_1\)

Tương tự \(\Delta COB\) cân \( \Rightarrow \widehat B_1 = \widehat C_2 \) mà \(OE// CF \Rightarrow \widehat B_1 = \widehat C_1\) (so le trong)

\( \Rightarrow \widehat C_2 = \widehat H_1 \Rightarrow HI//AC.\)

Lại có \(EI//OC\) (vì OEIC là hình bình hành) \( \Rightarrow EI\) và HI phải trùng nhau hay ba điểm E, H, I thẳng hàng \( \Rightarrow \) Ba điểm E, H, K thẳng hàng.