Cho tứ giác ABCD. Gọi E, F theo thứ tự là trung điểm của AB và CD; M, N, P, Q lần lượt là trung điểm của các đoạn thẳng AF, CE, BF và DE. Gọi I là giao điểm của MP và EF. Chứng minh rằng:
a) I là trung điểm MP.
b) MNPQ là hình bình hành.
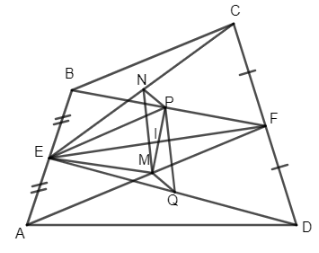
a) Ta có EP là đường trung bình của \(\Delta ABF\)
Advertisements (Quảng cáo)
\( \Rightarrow EP// AF\) và \(EP = \dfrac{1}{ 2}AF.\)
M là trung điểm của AF (gt)
\( \Rightarrow MF = \dfrac{1}{ 2}AF\)
Do đó \(EP//MF\) và EP = MF. Vậy EPFM là hình bình hành.
Advertisements (Quảng cáo)
I là giao điểm của MP và EF nên I là trung điểm của MP (1)
b) Tương tự ta chứng minh được \(EM//PF\) và \(EM = PF\) nên EPFM là hình bình hành \( \Rightarrow I\) là trung điểm của EF (vì I là trung điểm của MP)
Chứng minh tương tự ta có ENFQ là hình bình hành mà I là trung điểm EF \( \Rightarrow I\) là trung điểm của NQ
Từ (1) và (2) \( \Rightarrow MNPQ\) là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường thẳng).
