Bài 1: Cho tam giác ABC có \(\widehat B = {70^0},\widehat C = {60^0},\) vẽ đường cao AH. Hãy so sánh độ dài các đoạn HB và HC.
Bài 2: Cho tam giác ABC nhọn, hai trung tuyến BD và CE cắt nhau tại G. Gọi H, K lần lượt là trung điểm của GB và GC. Chứng minh DE // HK.
Bài 3: Cho tam giác ABC cân tại A (\(AB > AC\)), hai đường cao BD và CE cắt nhau tại H. Chứng minh:
a) \(\Delta AB{\rm{D}}\) và \(\Delta AC{\rm{E}}\) bằng nhau;
b) AH là đường trung trực của đoạn BC;
c) DE và BC song song với nhau;
d) \(AH > CH.\)

Bài 1:
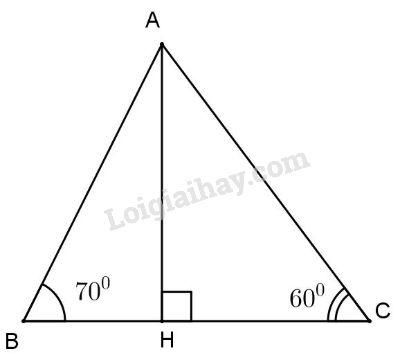
a) Ta có \(\widehat B > \widehat C\) (\({70^0} > {60^0}\) (gt)
\( \Rightarrow AC > AB\) (quan hệ góc cạnh trong tam giác)
\( \Rightarrow HC > HB\) (quan hệ đường xiên hình chiếu).
Advertisements (Quảng cáo)
Bài 2:
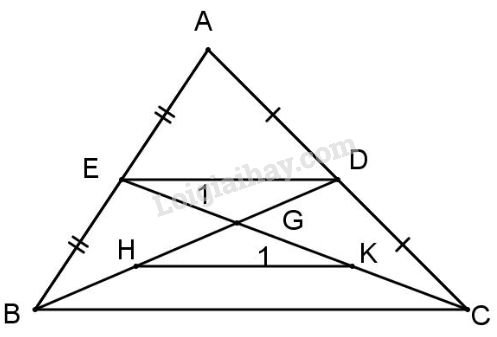
BD và CE là hai trung tuyến cắt nhau tại G nên G là trọng tâm \(\Delta ABC.\)
Ta có \(GB = 2G{\rm{D}}\) và \(GC = 2GE\) (tính chất trọng tâm);
H, K lần lượt là trung điểm của GB và GC (gt)
\( \Rightarrow GH = G{\rm{D}}\) và \(GK = GE.\)
Do đó \(\Delta {\rm E}G{\rm{D}} = \Delta KGH\) (c.g.c)
Advertisements (Quảng cáo)
\({\widehat E_1} = {\widehat K_1}\) (góc tương ứng)
Do đó ED // HK (cặp góc so le trong bằng nhau).
Bài 3:
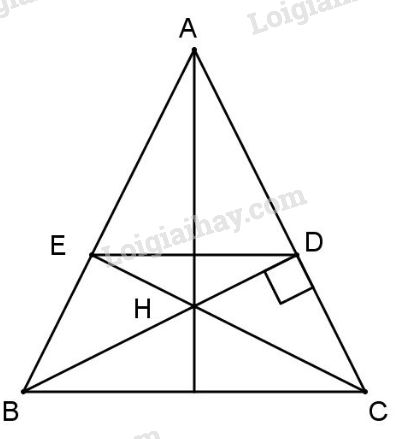
a) Xét \(\Delta A{\rm{D}}B\) và \(\Delta A{\rm{E}}C\) có
+) \(AB = AC\) (gt);
+) \(\widehat A\): chung.
Do đó \(\Delta A{\rm{D}}B = \Delta A{\rm{E}}C\) (cạnh huyền – góc nhọn).
b) BD và CE là hai đường cao của \(\Delta ABC\) (gt), mà BD cắt CE tại H là trực tâm.
Mặt khác, \(\Delta ABC\) cân tại A (gt) nên đường cao AH cũng đồng thời là đường trung trực của BC.
c) Ta có \(\Delta A{\rm{D}}B = \Delta A{\rm{E}}C\) (cmt)
\( \Rightarrow A{\rm{D}} = A{\rm{E}}.\) Do đó \(\Delta A{\rm{D}}E\) cân tại A, ta có
\(\widehat {A{\rm{ED}}} = \widehat {A{\rm{D}}E} = \dfrac{{{{180}^0} – \widehat A} }{ 2}\) (1).
Tương tự \(\Delta ABC\) cân tại A, ta có
\(\widehat {ABC} = \widehat {ACB} = \dfrac{{{{180}^0} – \widehat A} }{2}\) (2).
Từ (1) và (2) \( \Rightarrow \widehat {A{\rm{ED}}} = \widehat {ABC} = \dfrac{{{{180}^0} – \widehat A}}{ 2} \Rightarrow \)
ED// BC (cặp góc so le trong bằng nhau).
d) Ta có \(AB > BC\) (gt) \( \Rightarrow A{\rm{D}} > C{\rm{D}}\) (quan hệ đường xiên hình chiếu) \( \Rightarrow AH > CH.\)




![[Phòng GD Cẩm Giàng] thi học kì 2 môn Văn lớp 7 năm 2019: Tục ngữ có câu: “Ăn quả nhớ kẻ trồng cây”. Em hãy chứng minh tính đúng đắn của câu tục ngữ đó](https://dethikiemtra.com/wp-content/uploads/2020/08/1-100x75.jpg)

