Đề kiểm tra 15 phút lớp 9 môn Toán Chương 2 Hình học: Tính độ dài các dây AC, BC và bán kính đường tròn?

Cho đường tròn (O; R), đường kính AB cố định và dây AC. Biết rằng khoảng cách từ O lần lượt đến AC và BC là 8cm và 6cm.

a. Tính độ dài các dây AC, BC và bán kính đường tròn.

b. Lấy D đối xứng với A qua C. Chứng minh ∆ABD cân.

c. Khi C di chuyển trên đường tròn (O). Chứng minh rằng D thuộc một đường tròn cố định.

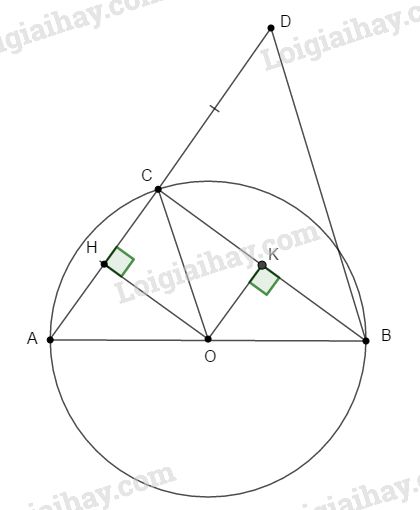
a. Kẻ OH, OK lần lượt vuông góc với AC và BC, ta có:

\(OH = 8cm, OK = 6cm\)

và \(HA = HC = {{AC} \over 2}\)

\(KB = KC = {{BC} \over 2}\)   (định lí đường kính và dây cung)

AB là đường kính nên \(\widehat {ACB} = 90^\circ \). Do đó tứ giác CHOK là hình chữ nhật (có ba góc vuông)

\(⇒ OH = CK = 8cm ⇒ BC = 16cm\)

Tương tự có : \(AC = 12cm\)

Xét tam giác vuông OHC, ta có:

\(OC = \sqrt {O{H^2} + H{C^2}}  = \sqrt {{8^2} + {6^2}}\)\(\;  = 10\,\left( {cm} \right)\) (định lí Pi-ta-go)

b. ∆ABD có đường cao BC đồng thời là đường trung tuyến nên ∆ABD cân tại B.

c. Ta có: \(BD = BA = 2R \) (cmt), B cố định, 2R không đổi.

Vậy D thuộc đường tròn cố định tâm B và bán kính bằng 2R.