Bài 12 chương 1: Giải bài 67,68,69 trang 31; bài 70,71,72,73,74 trang 32 SGK Toán 8 tập 1: Chia đa thức một biến đã sắp xếp và Luyện tập.
Ta trình bày phép chia tương tự như cách chia các số tự nhiên. Với hai đathức A và B của một biến, B ≠ 0 tồn tại duy nhất hai đathức Q và R sao cho:
A = B . Q + R, với R = 0 hoặc bậc bé hơn bậc của 1
– Nếu R = 0, ta được phép chia hết.
– Nếu R ≠ 0, ta được phép chia có dư.
Giải bài tập trong SGK bài 12 Toán 8 tập 1 trang 31, 32
Bài 67. Sắp xếp các đathức theo lũy thừa giảm dần của biến rồi làm phép chia:
a) (x3 – 7x + 3 – x2) : (x – 3);
b) (2x4 – 3x2 – 3x2 – 2 + 6x) : (x2 – 2).
HD: a) (x3 – 7x + 3 – x2) : (x – 3)
Sắp xếp lại: (x3 – x2 – 7x + 3 ) : (x – 3)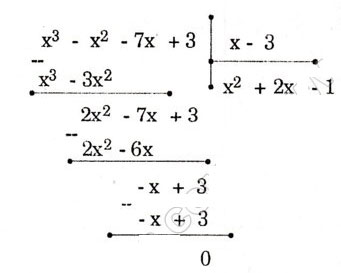
b) (2x4 – 3x2 – 3x2 – 2 + 6x) : (x2 – 2)
Sắp xếp lại: (2x4 – 3x2 – 3x2 + 6x – 2) : (x2 – 2)
Bài 68. Áp dụng hằng đẳng thức đáng nhớ để thực hiện phép chia:
a) (x2 + 2xy + y2) : (x + y);
b) (125x3 + 1) : (5x + 1);
c) (x2 – 2xy + y2) : (y – x).
HD: a) (x2 + 2xy + y2) : (x + y) = (x + y)2 : (x + y) = x + y.
b) (125x3 + 1) : (5x + 1) = [(5x)3 + 1] : (5x + 1)
= (5x)2 – 5x + 1 = 25x2 – 5x + 1.
Advertisements (Quảng cáo)
c) (x2 – 2xy + y2) : (y – x) = (x – y)2 : [-(x – y)] = – (x – y) = y – x
Hoặc (x2 – 2xy + y2) : (y – x) = (y2 – 2xy + x2) : (y – x)
= (y – x)2 : (y – x) = y – x.
Bài 69. Cho hai đa thức A = 3x4 + x3 + 6x – 5 và B = x2+ 1. Tìm dư R trong phép chia A cho B rồi viết A dưới dạng A = B.Q + R.
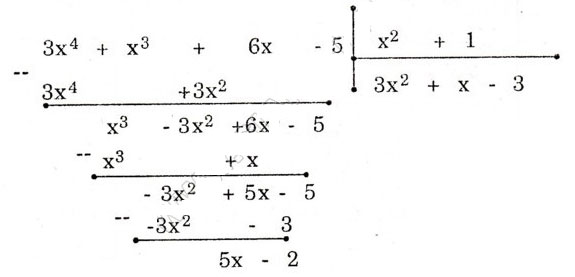
Vậy 3x4 + x3 + 6x – 5 = (x2+ 1)(3x2 + x – 3) + 5x – 2
Luyện tập
Bài 70. Làm tính chia:
a) (25x5 – 5x4 + 10x2) : 5x2;
b) (15x3y2 – 6x2y – 3x2y2) : 6x2y.
a) (25x5 – 5x4 + 10x2) : 5x2 = (25x5 : 5x2 ) – (5x4 : 5x2 ) + (10x2 : 5x2 ) = 5x3 – x2 + 2
b) (15x3y2 – 6x2y – 3x2y2) : 6x2y
= (15x3y2 : 6x2y) + (– 6x2y : 6x2y) + (– 3x2y2 : 6x2y)
Advertisements (Quảng cáo)
= 15/6xy – 1 – 3/6y = 5/2xy – 1/2y – 1.
Bài 71. Không thực hiện phép chia, hãy xét xem đathức A có chia hết cho đathức B hay không.
a) A = 15x4 – 8x3 + x2
B = 1/2x2
b) A = x2 – 2x + 1
B = 1 – x
HD: a) Ta có 15x4 ; 8x3 ; x2 chia hết cho 1/2x2 nên đa thức A chia hết cho B.
b) A chia hết cho B, vì x2 – 2x + 1 = (1 – x)2, chia hết cho 1 – x
Bài 72 Toán 8 tập 1. Làm tính chia:
(2x4 + x3 – 3x2 + 5x – 2) : (x2 – x + 1).

Khi đó :(2x4 + x3 – 3x2 + 5x – 2) = (x2 – x + 1)(2x3 + 3x – 2).
Bài 73. Tính nhanh:
a) (4x2 – 9y2) : (2x – 3y); b) (27x3 – 1) : (3x – 1);
c) (8x3 + 1) : (4x2 – 2x + 1); d) (x2 – 3x + xy -3y) : (x + y)
Đáp án: a) (4x2 – 9y2) : (2x – 3y) = [(2x)2 – (3y)2] : (2x – 3y) = (2x –3y)(2x +3y) : (2x –3y) = 2x + 3y;
b) (27x3 – 1) : (3x – 1) = [(3x)3 – 1] : (3x – 1) = (3x – 1) [(3x)2 + 3x + 1] : (3x – 1) = 9x2 + 3x + 1
c) (8x3 + 1) : (4x2 – 2x + 1) = [(2x)3 + 1] : (4x2 – 2x + 1)
= (2x + 1)[(2x)2 – 2x + 1] : (4x2 – 2x + 1)
= (2x + 1)(4x2 – 2x + 1) : (4x2 – 2x + 1) = 2x + 1
d) (x2 – 3x + xy -3y) : (x + y)
= [(x2 + xy) – (3x + 3y)] : (x + y)
= [x(x + y) – 3(x + y)] : (x + y)
= (x + y)(x – 3) : (x + y)
= x – 3.
Bài 74. Tìm số a để đathức 2x3 – 3x2 + x + a chia hết cho đathức x + 2
Giải bài 74:

Khi đó 2x3 – 3x2 + x + a = (x + 2) (2x2 – 7x + 15) + a – 30 để đa thức 2x3 – 3x2 + x + a chia hết cho đathức (x + 2) thì phần dư a – 30 = 0 hay a = 30.

![[THCS Phúc Chu] thi cuối học kì 2 lớp 8 môn Địa: Vẽ biểu đồ thích hợp thể hiện cơ cấu diện tích của ba nhóm đất chính của nước ta](https://dethikiemtra.com/wp-content/uploads/2020/06/canh-dong-100x75.jpg)



![[THCS Tân Đức] thi học kì 2 lớp 8 môn GDCD: Em hãy đóng vai một tuyên truyền viên để giải thích cho bạn bè và người thân hiểu tính chất nguy hiểm của hiểm của HIV/ AIDS](https://dethikiemtra.com/wp-content/uploads/2020/09/anh-dep-ve-thay-co-1-100x75.jpg)
