
Bài 1. Rút gọn các đa thức sau biểu thức:
a) \(A = \left( {{x^2} + 3} \right)\left( {{x^4} – 3{x^2} + 9} \right) – {\left( {{x^2} + 3} \right)^3}.\)
b) \(B = {\left( {x – 1} \right)^3} – {\left( {x + 1} \right)^3} + 6\left( {x + 1} \right)\left( {x – 1} \right).\)
Bài 2. Phân tích các đa thức sau thành nhân tử:
a) \(81{a^2} – 6bc – 9{b^2} – {c^2}\)
b) \({a^2} – 6{a^2} + 12a – 8.\)
Bài 3. Tìm x, biết:
\({\left( {x – 2} \right)^3} – \left( {x + 2} \right)\left( {{x^2} – 2x + 4} \right) + \left( {2x – 3} \right)\left( {3x – 2} \right) = 0.\)
Bài 4. Tìm m để đa thức \(A\left( x \right) = {x^3} – 2{x^3} + x – m + 2\) chia cho đa thức \(B(x) = x + 3\) có dư bằng 5.
Bài 5. Cho \(a + b = 1.\) Tính \({a^3} + {b^3} + 3ab.\)

Bài 1. a) \(A = {\left( {{x^2}} \right)^3} + {3^3} – {\left( {{x^2} + 3} \right)^3}\)
\(={x^6} + 27 – {x^6} – 9{x^4} – 27{x^2} – 27 \)
Advertisements (Quảng cáo)
\(= – 9{x^4} – 27{x^2}.\)
b) \(B = {x^3} – 3{x^2} + 3x – 1 – {x^3} – 3{x^2} – 3x – 1 + 6{x^2} – 6 \)\(\;= – 8.\)
Bài 2. a) \(81{a^3} – 6bc – 9{b^2} – {c^2} \)
\(= 81{a^2} – \left( {9{b^2} + 6bc + {c^2}} \right)\)
\(={\left( {9a} \right)^2} – {\left( {3b + c} \right)^2}\)
\(= \left( {9a + 3b + c} \right)\left( {9a – 3b – c} \right).\)
b) \({a^3} – 6{a^2} + 12a – 8 \)
\(= {a^3} – 3{a^2}.2 + 3a{.2^2} – {2^3} \)
Advertisements (Quảng cáo)
\(= {\left( {a – 2} \right)^3}.\)
Bài 3. Ta có:
\({\left( {x – 2} \right)^3} – \left( {x + 2} \right)\left( {{x^2} – 2x + 4} \right) + \left( {2x – 3} \right)\left( {3x – 2} \right)\)
\(={x^3} – 6{x^2} + 12x – 8 – {x^3} – 8 + 6{x^2} – 4x – 9x + 6\)
\(= – x – 10.\)
Vậy \( – x – 10 = 0 \Rightarrow x = – 10.\)
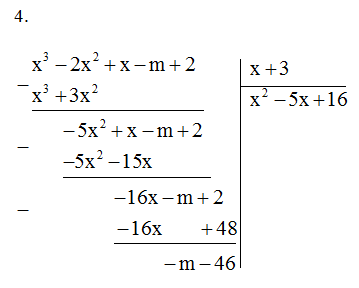
A(x) chia cho B(x) có dư bằng 5 \( \Rightarrow – m – 46 = 5 \Rightarrow m = – 51.\)
Bài 5. Ta có: \(a + b = 1 \Rightarrow b = 1 – a.\)
Vậy
\({a^3} + {b^3} + 3ab \)
\(= {a^3} + {\left( {1 – a} \right)^3} + 3a\left( {1 – a} \right)\)
\(={a^3} + 1 – 3a + 3{a^2} – {a^3} + 3a – 3{a^2}\)
\(= 1.\)





