Kiểm tra 1 tiết Chương 2 Đại số 9: Gọi A và B là giao điểm của đồ thị lần lượt với các trục tọa độ Ox, Oy. Tính diện tích tam giác OAB (O là gốc tọa độ).

Bài 1. Cho hàm số \( y=  – {4 \over 3}x – 4\)

a. Vẽ đồ thị của hàm số trên.

b. Gọi A và B là giao điểm của đồ thị lần lượt với các trục tọa độ Ox, Oy. Tính diện tích tam giác OAB (O là gốc tọa độ).

c. Tính góc α tạo bởi đường thẳng \(y =  – {4 \over 3}x – 4\) và trục Ox (làm tròn đến phút).

Bài 2. Cho hai đường thẳng : \(y = x – 1\) (d₁) và \(y = -x + 3\) (d₂).

a. Tìm tọa độ giao điểm M của (d₁) và (d₂).

b. Viết phương trình đường thẳng (d₃) song song với (d₁) và đi qua điểm \(N(0 ; 1)\)

c. Chứng tỏ rằng đường thẳng \(y = mx – 2m + 1\) luôn đi qua điểm M đã nói ở câu a khi m thay đổi.

Bài 1. a. Bảng giá trị:

Đồ thị của hàm số là đường thẳng qua hai điểm \(A(-3; 0)\) và \(B(0 ; -4)\)

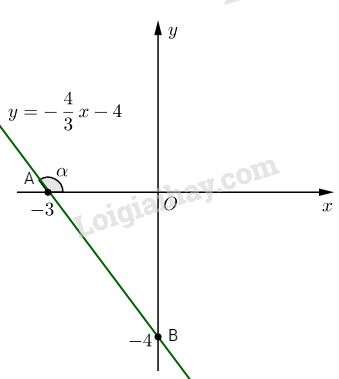
b. Ta có: \(OA = \left| { – 3} \right| = 3;OB = \left| { – 4} \right| = 4\)

\( \Rightarrow {S_{OAB}} = {1 \over 2}OA.OB = 6\) (đvdt)

c. Ta có: \(\alpha  = \widehat {TAx}\)

Trong tam giác vuông OAB, ta có:

\(\tan \widehat {OAB} = {4 \over 3} \Rightarrow \widehat {OAB} \approx 53^\circ 8′ \)

\(\Rightarrow \alpha  \approx 126^\circ 52’\)

Bài 2. a. Phương trình hoành độ giao điểm của (d₁) và (d₂) :

\(x – 1 = -x + 3 ⇔ 2x = 4 ⇔ x = 2\)

Thế \(x = 2\) vào phương trình của (d₁) \(⇒ y = 1\). Vậy \(M(2; 1)\).

b. (d₃) // (d­₁) nên (d₃) có phương trình: \(y = x + m (m ≠ -1)\)

\(N(0 ; 1) ∈ (d_3) ⇒ 1 = 0 + m ⇒ m = 1\) (nhận)

Vậy phương trình (d₃) là : \(y = x + 1\).

c. Thế tọa độ \(M(2; 1)\) vào phương trình \(y = mx – 2m + 1\), ta được:

\(1 = 2.m – 2m + 1\) (luôn đúng với mọi m)

Vậy đường thẳng \(y = mx – 2m + 1\) luôn đi qua M.