
Bài 1. Cho đường tròn đường kính AB. Kẻ dây CD vuông góc với AB tại điểm I bất kì trên AB. Nối I với trung điểm M của AD. Chứng minh MI vuông góc với BC.
Bài 2. Cho đường tròn (O) đường kính AB. Điểm C nằm giữa A và O. Vẽ đường tròn (O’) có đường kính là CB.
a. Hai đường tròn (O) và (O’) có vị trí tương đối như thế nào ?
b. Kẻ dây DE vuông góc với AC tại trung điểm H của AC. Chứng minh rằng tứ giác ADCE là hình thoi.
c. Gọi K là giao điểm của BD với đường tròn (O’). Chứng minh rằng ba điểm E, C, K thẳng hàng.
d. Chứng minh rằng HK là tiếp tuyến của đường tròn (O’)

Bài 1.
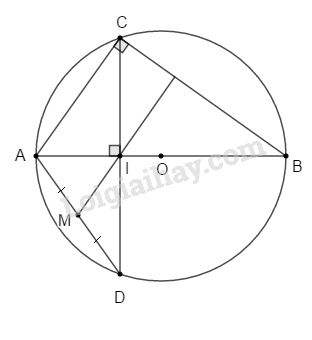
Ta có: \(CD ⊥ AB\) tại I \(⇒ IC = ID\) (định lí đường kính dây cung).
Advertisements (Quảng cáo)
Lại có M là trung điểm của AD (gt) nên IM là đường trung bình của ∆ACD
\(⇒ IM // AC\) (1)
Mà \(\widehat {ACB} = 90^\circ \) (AB là đường kính)
hay \(AC ⊥ BC\) (2)
Từ (1) và (2) ta có: \(MI ⊥ BC\)
Bài 2.

Advertisements (Quảng cáo)
a. Ta có: \(OO’ = OB – O’B\) (\(d = R – R’\)) \(⇒ (O)\) và \((O’)\) tiếp xúc trong tại B.
b. Ta có: \(DE ⊥ AC\) tại trung điểm H
\(⇒ HD = HE\) (định lí đường kính dây cung)
Do đó tứ giác ADCE là hình thoi.
c. Ta có: \(\widehat {ADB} = 90^\circ \) (AB là đường kính)
hay \(AD ⊥ BD\), mà EC // AD
\(⇒ EC ⊥ BD\) (1)
Lại có \(\widehat {CKB} = 90^\circ \) (CB là đường kính)
hay \(CK ⊥ BD\) (2)
Từ (1) và (2) \(⇒ EC\) và \(KC\) phải trùng nhau.
Vậy ba điểm E, C, K thẳng hàng.
d. Ta có: \(∆BO’K\) cân tại O’ (\(O’B = O’K = R’\)) \( \Rightarrow {\widehat B_1} = {\widehat K_1}\,\left( 3 \right)\)
\(∆EKD\) vuông có HK là đường trung tuyến nên \(HK = HE = {1 \over 2}ED\)
\(⇒ ∆EHK\) cân \( \Rightarrow {\widehat E_1} = {\widehat K_3}\,\left( 4 \right),\,ma\,{\widehat E_1} = {\widehat B_1}\,\left( 5 \right)\) (cùng phụ với \(\widehat {EDB}\) )
Từ (3), (4) và (5) \( \Rightarrow {\widehat K_1} = {\widehat K_3},\) mà \({\widehat K_2} + {\widehat K_1} = 90^\circ \Rightarrow {\widehat K_3} + {\widehat K_2} = 90^\circ \)
hay \(HK ⊥ O’K\). Chứng tỏ HK là tiếp tuyến của (O’)


![[THCS Bình Giang] kiểm tra môn Sử lớp 9: Em hãy trình bày ngắn gọn diễn biến, kết quả của chiến dịch lịch sử Điện Biên Phủ năm 1954?](https://dethikiemtra.com/wp-content/uploads/2019/03/dongphongnha-100x75.jpg)

![[TX An Nhơn] thi học kì 2 lớp 9 môn Văn năm 2020: Tác phẩm “Những ngôi sao xa xôi” được Lê Minh Khuê viết vào năm nào?](https://dethikiemtra.com/wp-content/uploads/2020/06/canh-dong-100x75.jpg)
