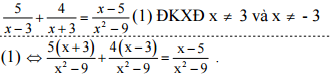Đáp án chi tiết đề thi cuối học kì 2 lớp 8 môn Toán của Phòng GD & ĐT Huyện Đại Thành. Xem đề và đáp án tại đây
Câu 1 (3,0 điểm): Giải các phương trình sau:
a) 2x – 3 = 0 b) (2x – 6)(3x + 15) = 0.
Câu 2 (1,0 điểm): Cho hai số thực a, b thỏa mãn a ≤ b. Chứng minh rằng:
a) 2015a – 2016 ≤ 2015b – 2016 b) -2015a – 2016 > -2015b – 2017
Câu 3 (2,0 điểm): Một ô tô đi từ A đến B với vận tốc 40 km/h. Sau khi đi đến B và nghỉ lại ở đó 30 phút, ô tô lại đi từ B về A với vận tốc 30 km/h. Tổng thời gian cả đi lẫn về là 9 giờ 15 phút (kể cả thời gian nghỉ lại ở B). Tính độ dài quãng đường AB?
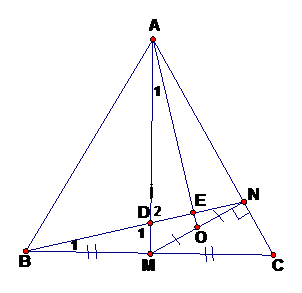
Câu 4 (3,0 điểm): Cho tam giác ABC cân tại A. Gọi M là trung điểm của cạnh đáy BC, N là hình chiếu vuông góc của M trên cạnh AC và O là trung điểm của MN. Chứng minh rằng:
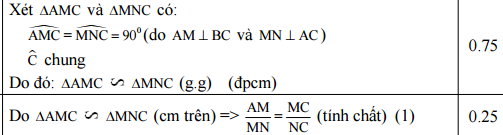
a) Tam giác AMC đồng dạng với tam giác MNC.
b) AM.NC = OM.BC
c) AO ⊥ BN
Câu 5 (1,0 điểm): Giải phương trình:
Đáp án
Câu 1:
a) 2x – 3 = 0 <=> 2x = 3 (0,25đ)
<=> x = 3/2 (0,25đ)
Vậy tập nghiệm của phương trình là S = { 3/2} (0,25đ)
Advertisements (Quảng cáo)
b) (2x – 6)(3x + 15) = 0 <=> (2x – 6) = 0 hoặc (3x + 15) = 0 (0,25đ)
* (2x – 6) = 0 <=> x = 6/2 = 3 (0,25đ)
* (3x + 15) = 0 <=> x = – 15/3
Vậy tập nghiệm của phương trình là S = {3; -5} (0,25đ)
c) <=> 24 + 3x – 15 = 8x – 2 (0,25đ)
<=> – 5x = – 11 (0,25đ)
<=> x = 11/5
Vậy tập nghiệm của phương trình là S = {11/5} (0,25đ)
d)
Suy ra 8x = – 8 <=> x = – 1(TM) . (0,25đ)
Advertisements (Quảng cáo)
Vậy tập nghiệm của phương trình là S = {– 1} (0,25đ)
Câu 2
a) Ta có: a ≤ b <=> 2015a ≤ 2015b (0,25đ)
<=> 2015a – 2016 ≤ 2015b – 2016
Vậy 2015a – 2016 ≤ 2015b – 2016 (0,25đ)
b) Ta có: a ≤ b <=> -2015a ≥ -2015b <=> -2015b – 2016 ≥ -2015b – 2016 (0,25đ)
Mà -2015b – 2016 > -2015b – 2017 => -2015a – 2016 > -2015b – 2017
Vậy -2015a – 2016 ≥ -2015b – 2017 (0,25đ)
Câu 3: Đổi: 30 phút = 1/2giờ ; 9 giờ 15 phút = 37/4 giờ. (0,25đ)
Gọi độ dài quãng đường AB là x km (x>0) (0,25đ)
Vì ô tô đi từ A đến B với vận tốc 40 km/h nên:
Thời gian ô tô đi từ A đến B là x/40 (giờ) (0,25đ)
Vì ô tô đi từ B về A với vận tốc 30 km/h nên:
Thời gian ô tô đi từ B về A là x/30 (giờ) (0,25đ)
Vì tổng thời gian cả đi lẫn về là 9 giờ 15 phút (kể cả thời gian nghỉ lại ở B) nên, ta có phương trình: (0,5đ)
Giải phương trình (*) tìm được x = 150 (TM) (0,25đ)
Vậy độ dài quãng đường AB là 150 km. (0,25đ)
Câu 4: Hình vẽ (0,25đ)
a) Vì ΔABC cân tại A, có M là trung điểm của BC (gt) nên AM là đường trung tuyến đồng thời cũng là đường cao của tam giác ABC
=> AM ⊥ BC
Câu 5: