Đề kiểm tra 15 phút môn Toán – Chương 1 Hình học 8: Gọi E là giao điểm của AI và BJ, giả sử E thuộc cạnh CD, chứng minh: CD = AD +BC

Cho hình thang ABCD \(\left( {AB//CD;AB < CD} \right),\) các tia phân giác của góc A và D cắt nhau tại I, các tia phân giác của góc B và C cắt nhau tại J.

a) Chứng minh \(AI \bot DI\) và \(BJ \bot CJ\)

b) Gọi E là giao điểm của AI và BJ, giả sử E thuộc cạnh CD. Chứng minh: \(CD = AD +BC.\)

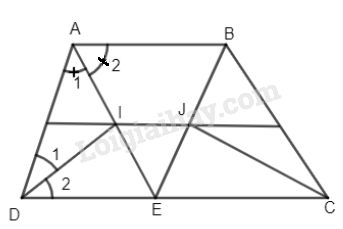
a) \(\widehat {{A_1}} = \widehat {{A_2}}\,(gt)\)

\(\widehat {{D_1}} = \widehat {{D_2}}\,(gt)\) mà \(\widehat A + \widehat D = {180^ \circ }\)

                     \( \Rightarrow \widehat {{A_1}} + \widehat {{D_1}} = {90^ \circ }\)

Trong \(\Delta AID \Rightarrow \widehat {AID} = {180^ \circ } – {90^ \circ } = {90^ \circ }\) hay \(AI \bot DI\)

Tương tự ta chứng minh được \(BJ \bot CJ\)

b) Xét \(\Delta AID\) có phân giác DI đồng thời là đường cao (cmt)

\( \Rightarrow \Delta ADE\) cân tại D \( \Rightarrow AD = DE\)  Tương tự ta có \(BC = EC\).

Mà \(DC = DE + EC \Rightarrow DC = AD + BC\) (đpcm)